为何回归方程的常数是负值？

L君 @ 2009-11-18:

老师，您好，我在做毕业论文。问题简化后说就是：有两个不同组别的多元线性回归方程进行比较

y1=a1+b1X1+c1X2+d1X3

y2=a2+b2X1+c2X2+d2X3

1，2为两个不同的大区域（每个大区域都有40个小区域作为观测值）；y为污染总量，X1, X2, X3为三种类型的污染源面积（工厂，工地，居民区），b, c, d为三种污染源的单位面积污染量（在模型里都为正数）。现在需要比较1，2两地的污染状况，三种类型污染源的污染贡献量等。我得到的两个回归方程，b、c、d都为正数，但是常数项a1为正，a2为负。这样对单位污染量的比较有影响吗？可以这么分析吗？在这个分析中，可不可以给出非标准回归系数的回归方程，然后用标准回归系数（常数项为0）解释贡献量？但是单位面积污染量要继续用于后续计算的话，是用标准还是非标准的回归系数呢？

但是，如果 y1＝30＋2X1＋3X2＋4X3、y2＝－300＋20X1＋30X2＋40X3，在两个区域，2区域的单位面积的效益就明比1大，但是在3类污染源面积相同的情况下，y总值是一样的？这个就不太好解释了。其实就算是都为正，但是相差较大的话，也不能比较区域1，2的单位面积效益大小？怎么解决这个问题呢？

还有，这个模型的R平方，还有sig等检验系数有的不合格。之后我改用偏最小二乘法，用SPSS和SIMCA-P计算结果都和多元线性回归得到的方程一样。那是不是随便用哪个结果都行呢？

庄主 @ 2009-12-06:

你提到了好几个问题，其中第一题：两个样本的所有自变量和因变量（污染值或面积）取值都应该是非负值、或许都是正值（960万平方公里之内哪里还有0污染的净土？），但是两个对应回归方程的常数项a1为正、a2为负。你问：这对样本之间“单位污染量”的比较有影响吗？我这学期教的同学中也有问过：“变量全部为正值、为什么回归方程常数为负值？我觉得后者问题更有普遍意义，所以本贴主要谈这个问题，你的其余问题放在最后简单说一下。

我们知道，常数项b0（你用a来表示，为了与本庄其它帖子一致，这里用b0）反映的是当所有自变量分别取值为0时因变量Y的值。但是，在很多实际研究中，出现负值的b0是一件很奇怪或很尴尬的事。在本例中，如果自变量X1-X3（工厂、工地、居民区）没有污染面积，那么该区域不仅没有任何污染而且还会“负污染”（世上真有比蓝天、绿地、白云更圣洁的境界？），真的很奇怪。其实，这仅仅是有关变量的取值区间及其关系强度之间的特定搭配而造成的错位而已。

我们先从下图中获得一些直观的认识。图中的两条线分别代表一个回归方程，其中A线是向上的（即b1为正），但它在X = 0时Y < 0（即b0为负）；相反，B线是向下的（即b1为负），而它在X = 0时Y < 0（即b0也为负）。说明b0的取向与b1没有直接关系。另外，A的数据可以局限在A1-A2范围内，即X和Y全部为正值；也可以局限在A3-A4范围内，即X和Y全部为负值。反之，B的数据可以局限在B1-B2范围内，即X为全为负值而Y全为正值；或者局限在B3-B4范围内，即X全为正值而Y全为负值。当然，如果数据局限在A2-A3或B2-B3范围内，X和Y即可为正也可为负。以上六种情况，穷尽了X和Y的可能取值，但其回归方程的常数b0总是为负，说明b0的取向与X和Y的取值范围也没有直接关系。

那么，b0的取向到底受什么影响？其中有什么规律可循？我查了一些教科书，希望找到一个权威的说法来引用一下，可惜还没有查到（也许我查的不够广泛和彻底）。以下是我的推导，尚未得到“权威”认可，仅供大家参考。

我们从简单回归方程出发：

Y = b0 + b1X             (1)

如重新组织公式1即有：

b0 = Y – b1X              (2)

我们知道，如果b1已知（通过回归分析而得知）、就可以将Y和X的任意一对常数（如两者的均值、最大值、最小值、均值之一个标准差之上或之下、等等）分别代入公式2而求出b0。这里，我们分别用Y和X的最小值（记为“Ymin”和"Xmin”）来代入公式2：

b0 = Ymin – b1Xmin   (3)

很显然，Ymin、Xmin和b1可以取任何值而公式3均可成立，这与我们从上图得到的直观理解是一致的。更重要的是，我们可以从公式3推导出b0取负值的条件：如果 b0 < 0, 那么Ymin – b1Xmin < 0, 也即 

b1Xmin > Ymin          (4)

或者，

b1 > Ymin/Xmin        (5)

公式4告诉我们，如果Ymin小于Xmin与b1的乘积，那么该回归方程的常数b0为负值；而公式5则直接显示，如果Ymin与Xmin的比值小于b1，那么b0为负值。（当然，我们将公式4和5中的“>”改成“<”或“=”，则可得到b0为正值或为0的条件，但因为后两者属于“正常”现象，所以不再赘言。）

好了，我希望大家至此明白b0为负实属正常情况，即不代表任何“负相关”、也不反映任何数据问题，而是我一开始说的那样：“有关变量的取值区间及其关系强度之间的特定搭配而造成的错位而已”。所谓“错位”，其实只是“错觉”而言。

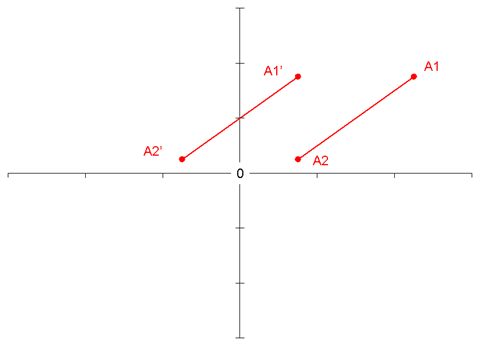
当然，这种错觉有时很难向读者交代或解释清楚，尤其是在A1-A2数据的情况下，出现一个负b0总会令人质疑的。有何解决方法？有，很简单，就是对X取中值（centering，详见本庄前贴）。X取中值后，回归方程的斜率b1保持不变，但b0会变，其已经不再是X = 0时Y的值，而是X=均值时Y的值。如果数据是A1-A2段的话，那么X的均值一定是正的，所以b0也一定为正（见下图，其中A1’和A2’分别为A1和A2的取中值）。

最后简单回答一下L君的其它问题。

一、虽然你的a1为正、a2为负，但两个方程仍然是直接可比的。a1为正、a2为负的意思是，区域1的“污染起点”（即在没有受到X1-X3的任何影响下）高于区域2（也许因为还有其它污染来源）。当然，如果你对两个样本的X1-X3都取中值后，a1和a2应该全部为正，看起来好像更可比，但它们之间的差别应该与现在的差别完全一样。当然，取中后的a1和a2的解读有所变化，反映的是自变量X1-X3各自为均值（即工厂、工地和居民区平均污染水平）时该区域的污染总量。

二、比较两个方程，应该用非标准化回归系数（b）、而不是非标准化回归系数（Beta），因为b反映了X和Y的关系强度，而Beta则是用以下公式从b转换而来：

Beta = bSDx/SDy         (6)

其中SDx和SDy分别是X和Y的标准差。我们知道，两个样本之间的X或Y的标准差会因为各自样本大小、异常值（如区域1有一个超大的异常值或区域2有一个超小的异常值）等因素而不同，所以即使两个样本的b相等，它们的Beta也很可能不等。所以，比较不同方程之间的Beta是没有意义的。

如果你想比较X1-X3在两个区域的各自独立贡献(net contribution)，可以比较每个X与Y的semipartial correlation coefficient之平方（在SPSS回归中叫做PART）。

三、如果你的数据满足了线性回归（OLS）的要求，那么OLS回归的结果是“蓝色的”（best linear unbiased estimate，间称BLUE，即最佳无偏线性估计），所以应该报告OLS回归结果。

如何提高间接影响模型的效应？（更新版）

hz @ 2009-11-30:

我提出了一个理论模型（见下图），假设A通过B和C对D有间接影响。实证数据表明，A->B、B– C、C–>D的影响都显著，但是三者的乘积（即A–>D的间接影响）却不显著。另外，A–>D的直接影响也显著。不知有无方法提高间接影响？是否可以将显著水平从0.05放宽到0.10？

庄主 @ 2009-12-04:

你的理解对了一部分，即A–>D的间接影响包括A–>B–>C–>D的所有回归系数之连续乘积 (= 0.30 x 0.20 x 0.10 = 0.006)。但在你的模型中，A->D之间其实有三条间接路径：一是你说的A–>B–>C–>D；二是A–>B->D；三是A–>C–>D（见下图）。

如果你的理论规定A–>D的间接影响只能有A->B->C->D一条路径，是否可以？当然可以。但你须要预期到如此假设更难被证实。如果你的理论容许，那么加上A->B->D和A->C->D的间接影响之后会如何？一切取决于A->C和B->D的系数强度。你可以代入一些可能发生的数值来计算A->D的总间接影响。如，

1. A->B = 0.20和B->D=0.20，总间接影响=0.086，可能不显著，同时也小于A->D的直接影响；
2. A->B = 0.30和B->D=0.30，总间接影响=0.126，虽然仍小于A->D的直接影响，但可能显著，属于“弱间接影响”（参见前贴“如何检验两个中介变量的效应? ”http://zjz06.blogspot.com/2009/04/blog-post_25.html或http://zjz06.spaces.live.com/blog/cns!3F49BBFB6C5A1D86!1159.entry）；
3. A->B = 0.40和B->D=0.40，总间接影响=0.166，可能显著，并大于A->D的直接影响，属于“强间接影响”。

当然，基于你现有的回归系数均在0.10到0.30之间，我怀疑即使将后两条间接路径等间接影响（假定两个未知的系数也在0.10到0.30之间）加进去，总间接影响还可能不显著。总之，间接影响模型在理论上很诱人、但在实证上要求很高，尤其是多阶段间接影响模型，一般都很难证明。

最后，你问是否可以将显著水平条件放宽到0.10？答案是否定的。一、统计决策的显著水平（α）是在检验之前就要设置的，而不能在检验之后、因实证显著水平p大于α而将α提高。二、α一般设为0.05，代表犯Type I 错误的概念有5%，如果提高到0.10，则将Type I 错误提高到10%，除了初步的探索性研究之外，这种错误率太高。三、结构方程模型中的回归系数已经修正了测量误差，所以一般不应该再放宽其显著水平。

hz @ 2010-01-17:

在上次关于直接效应和间接效应的问题，我还有一个地方不明白：如何判断间接效应是在一定置信水平上显著？以A->B->C–>D为例，判断三者的乘积（即A–>D的间接影响）是否意味将A,B,C同时放入对D的回归方程，三者回归系数分别达到显著水平？

庄主 @ 2010-01-24:

文献上有过类似说法，但从未被证明过。现在一般的做法是用Bootstrapping求出三系数乘积 (如a x b x c)的standard error (如记为”se(abc)”) 的经验估计值，然后计算 abc/se(abc)的比率，该值也是服从t-分布的。AMOS里有Bootstrapping。

如何确定名目变量交互项的参照组是什么？

台灣吳同學 @ 2009-11-13:

老師您好,我是台灣的學生,對您的統計解釋相當有興趣。最近我遇到了一個問題,我嘗試把他說清楚,希望您可以幫我解惑。

在我的logit model裡頭,有兩個類別變數，分別為性別與教育程度。其中,性別是男女二分變數(男=1,女=0),而教育程度則分為低,中,高三類(中=0).我的依變數是收入,分為低與高兩種(低=0).假設,我想探討性別與教育程度的交互作用(性別X教育程度),我的交互作用項只能把1.男X低教育和2.男X高教育放入模型中,請問我的交互作用項在這時候的參照類是什麼?是1.男X中教育? 還是2.女X中教育?

另外,也想知道要如何解讀交互作用項B和EXP(B)的意義。希望您能看得懂我的問題,謝謝!

庄主 @ 2009-11-15:

吴同学，从统计上来说你的问题并不难，但要解释清楚却简短不了，而且有点绕弯弯（所以提醒读者随手做些推算验证，以免绕不出来）。我把这类问题叫做technically simple but practical not trivial (技术上很容易但操作上不简单)，往往会被人疏忽或轻视，所以不容易找到答案。如你问的，实质上是一个“如何解读回归分析中交互项的系数？”的问题，对此我已写过好几个帖子（如“如何在回归分析中检验和解读交互影响？”）。但是，你由于下面谈到的若干误解而对这个问题产生困惑，也许已问过其他人或查过其它参考文献，但却不得而知。

我觉得你的困惑可能有三个来源混合而成：第一，你的因变量(dependent variable)不是收入本身、而是高收入与低收入之比例的对数，但无论你根据什么理由来如此构建因变量，你的问题与因变量性质无关，也就是说交互项的对照组问题在包括OLS、GLS、Logit、Probit、Logistic等等所有回归分析中是一样的。所以有关如何解读回归分析交互影响的文献（包括我自己的有关帖子）都是直接相关的。

第二，你的两个自变量都是nominal scale (名目变量) 而不是更常见的interval scale (等距变量)，而且你用了dummy coding（哑变量编码）方法，但你对这种编码的原理了解不够（很多人都有同样问题），所以无法将如何解读定距变量交互影响的文献转换成你的答案。

第三，也许是最重要的，是你将交互影响等同于main effects（主效应）影响了。此话怎讲？你知道一个名目自变量转换成哑变量之后，其回归系数描述的是该哑变量取值为1的“研究组”与取值为0的“对照组”之间在因变量Y的平均值上的差别。这种理解完全正确。但是，你将其推广到对交互项系数的理解上去了，所以会问该系数是跟哪个对照组在比较？

为了有助其他读者理解你的问题，我用以下公式来表述你的回归模型：

Y = b0 + b1M + b2H + b3L + b4MH + b5ML                         (1)

其中，Y是因变量的平均值（注意：为了写作方便，本文没有按惯例在Y上加一横杆来代表平均值），M是性别（因为Male=1，所以命名为M），H是高教育程度（High），L是低教育程度（Low），MH是你说的“男X高教育”的交互项，ML是“男X低教育”的交互项。b0是在性别和教育两个变量中同时担任对照组（即同时取值为0）的FM（女性中等教育）组的均值，b1是男女差别（即性别的主效应，注意：这句话在有交互影响条件下有问题的，见后面的简单讨论）、b2是高教育与中教育的差别（高教育主效应，注意：这句话在有交互影响条件下也是有问题的，见后面的简单讨论）、b3是低教育与中教育的差别（低教育主效应）、b4是性别与高教育的交互影响、b5是性别与低教育的交互影响。

上面这段话中，大都分都是常识，唯一需要加以讨论的是什么叫做“性别与高（或低）教育的交互影响”。以b4为例，它反映的是“性别对高等-中等教育程度之间差别的影响”、或倒过来说，是“高教育对男女之间差别的影响”（这两种说法是等价的）。也就是说，b4描述的是高和中教育组之间的差别大小、在男性和女性之间是否相同；或者，男女之差的差别大小在高和中两组之间是否相同。这个意思，中文里说确实有点绕弯弯，用英文表述则相当清楚: b4 indicates whether the difference between the highly-educated and moderately educated groups is constant (uniform, equivalent, invariant, etc.) for men and women, respectively; or whether the difference between men and women is constant (…) for highly educated and moderately educated people, respectively. 

这是问题的核心：主效应系数（b1-b3）反映的是组间差别，所以有研究组和对照组；但是交互项系数（b4-b5）反映的是组间差别的差别（difference between diffrences between groups, or difference between group-differences)，所以没有主效应系数意义上的对照组。也就是说，b4或b5反映的不是两个组之间是否有差别，而是两个组间差别之间是否有差别，所以不需要有、也不可能只有一个对照组。

问题解决了吗？应该还没有。我希望大家能够记住两句话：一、交互项系数反映的是交互影响而不是组间差别（即“交互影响不等于组间差别”）；二、组间差别又是与（显著的）交互影响直接有关的。为了说明第二句话，我们来看看在交互项显著的条件下组间差别是如何计算的。我们可以根据模型1，写出计算你的六个组（= 2个性别组 x 3个教育组）的平均值Y的公式：（请大家拿出纸和笔来，将0和1值分别代入模型1，以复核实下述公式。光看不练，也许越看越迷糊。）

男高(MH):	YMH=b0 + b1x1 + b2x1 + b3x0 + b4x1x1 + b5x1x0 = b0 + b1 + b2 + b4	(2)
男中(MM):	YMM=b0 + b1x1 + b2x0 + b3x0 + b4x1x0 + b5x1x0 = b0 + b1	(3)
男低(ML):	YML=b0 + b1x1 + b2x0 + b3x1 + b4x1x0 + b5x1x1 = b0 + b1 + b3 + b5	(4)
女高(FH):	YFH=b0 + b1x0 + b2x1 + b3x0 + b4x0x1 + b5x0x0 = b0 + b2	(5)
女中(FM):	YFM=b0 + b1x0 + b2x0 + b3x0 + b4x0x0 + b5x0x0 = b0	(6)
女低(FL):	YFL=b0 + b1x0 + b2x0 + b3x1 + b4x0x0 + b5x0x1 = b0 + b3	(7)

模型2-7告诉我们如何计算六个组的平均值。为了便于计算它们之间的差别（更重要的是洞察它们之间的结构性关系），我们将模型2-7按以下方式重新安排一下：

表一、性别与教育程度交叉组的回归系数比较

	M（男性）	F（女性）
H（高教育）	b0 + b1 + b2 + b4   (2)	b0 + b2       (5)
M（中教育）	b0 + b1                 (3)	b0              (6)
L（低教育）	b0 + b1 + b3 + b5   (4)	b0 + b3       (7)

根据表一，我们可以很轻松地（目测）算出各组的差别。基于共有六组，共有 6 x 5 / 2 = 15对组组比较，我们用以下的矩阵形式来表示，以省些空间：

表二、组间差别之计算方法

	MH	MM	ML	FH	FM
MM	b2+b4
ML	b2+b4–b3-b5	-b3-b5
FH	b1+b4	b1–b2	b1+b3+b5-b2
FM	b1+b2+b4	b1	b1+b3+b5	b2
FL	b1+b2+b4-b3	b1-b3	b1+b5	b2-b3	-b3
注：所有组间差别均由column group – row group（列标题中的组减去行标题中的组）构成。如MH-MM = b2+b4。如果想求行组减列组，只需将表二中所有系数的符号相反即可。

由表二可知，只有三对组间差别是直接由回归系数告知的 (MM - FM = b1, FH – FM = b2, FM – FL = –b3；注意，这里的b1只反映中等教育程度上男女之间的差别、而不是所有教育程度上的男女差别；b2和b3只反映女性中不同教育程度的差别、而不是所有人中不同教育程度的差别，这就是我前面提到的对主效应系数的一般解释“在有交互影响条件下有问题的”的原因)，而且三者均只涉及主效应系数。另有两对组间差别是由两个主效应系数的组合而成 (MM – FL = b1 – b3, FH – FL = b2 – b3)。其它10对组间差别均涉及主效应和交互项系数的组合。其中尤其是MH - MM的差别，需要同时用到b4和b5两个交互项系数。

这个练习说明什么？既说明交互项系数不等于组间差别、又说明（大部分）组间差别与交互项系数有关系。具体说来，这种“关系”，是附加在主效应系数的基础上产生的，也就是说交互项系数是对一对主效应关系的adjustment（调整）。其调整程度（微调或巨调）则有b4或b5取值决定。

现在，问题解决了吗？也许有些读者还是有点迷糊，觉得名目变量交互分析好麻烦。对的，这就是我一开始说的“技术上容易操作上难”的道理。推而广之，凡涉及名目变量的多元分析（如loglinear modeling、multinomial logistic regression、等等），没有一样不是技术上容易操作上难的。大家要有充分的心理准备。

在本例中，将问题变得相对简单（或容易？）一些的一种方法是不用哑变量编码、而用effects coding（效应编码？）或 contrast coding（配对编码？）。前者用+1定义研究组、-1定义对照组；后者则按一定的限定条件（恕不赘言）来设定任意两组或两集合组（如本例中高教育对中低教育）的比较。由两个效应编码变量构成的交互项反映了在该两个变量上取值为+1的研究组与所有组的（未加权）均值（虽然不一定等于样本均值、但接近“平均”的意思）之差别（如在本例中，可以是男性高教程度与样本“平均”的差别）；由两个配对编码变量构成的交互项则反映了被特定配对的两组或两集合组之间的差别（在这种条件下，交互项系数可以等于组间差别了）。当然，这两种编码（尤其是后者）比哑变量编码在操作上复杂很多、但好处是解读时简单。如果有意学习（或者经常要做）名目变量多元分析的读者，应该花时间分别学一下。（当然，必须说明，不够使用哪种编码方法，交互项的显著性结果是完全一样的。它们的差别只存在于SPSS或其它统计程序输出结果中的系数值，而不同的系数值都是可以互相换算的。）

结束前，为完整起见，需要说明，这里虽然只讨论两个名目变量之间的交互项，其原则可以直接推广到三个或更多个名目变量之间的交互项。

最后，你问如何解读“交互作用項B和EXP(B)”，上面已经讨论了b4-b5的解读。Exp(b)的解读与其相仿，唯一区别在于后者的临界点为1而前者为0，如Exp(b4) > 1或Exp(b5) > 1 反映教育程度的差别在男性中大于女性；相反，如Exp(b4) < 1或Exp(b5) < 1则反映教育程度的差别在男性中小于女性。

如何判断统计显著的差别是否具有实际意义？

丁丁 @ 2009-10-02：

老师，您好！我想问一个关于样本量的基础问题。通常我们有公式可以计算理论最小样本量。但我想问有没有最大样本量，不得因为如果样本量足够大，我可以证明任何没有实际意义的差别是不是statistically significant。比如说，3.75和3.50，SD 都为1.00，如果样本量个为100，不显著。如果是200，就显著了。同理，3.50和3.55，如各有10000，也显著了。但是没有实际意义。我看到很多研究就用这种方法，研究出了很多correlation significant的结果，或两者显著不同的结论。我觉得不对，却没有理论去说它不对。难道真如某人所说, 统计学家可以证明任何事吗?

庄主 @ 2009-10-31:

抱歉，拖了将近一个月才回复你的问题。最近较忙，忙的原因之一是做有关博客写作的可持续性研究（好像就是在研究我自己为什么不能持续写博客）。

你的问题涉及了样本量和统计显著性两个概念，为了理解两者之间的关系，还需要引入其它三个概念：errors in inferential decision（推断决策中的错误）、power of analysis （检验效能）、strength of relationship 或effect size（关系强度或效应规模，注1）。

我们从统计显著性开始，因为大家在看一个统计分析（如相关、回归、方差等）的结果时，总是首先看其显著性（即p值是否小于预设的α值，如 0.05），然后据此而做出相应的推断决策。如p<α则拒绝零假设、p>α则接受零假设。大家知道，尽管有上述p值做依据，这种决策还可能含有误差。如当p<α时，也许零假设还是对的，这时就有犯概率为p的Type I error（型一或“拒真”错误）。相反，如当p>α时，也许零假设却是错的，这时就有犯概率为1 - p的Type II error（型二或“纳伪”错误）。相信大家都看过这些老套的话，但也许不知道这些老土道理是解决很多困惑（包括丁丁的问题）的基本原理。

丁丁关心的是在大样本条件下犯型一错误的可能性。我们先看一下他（她）的例子：有两个均值，分别为3.7和3.5，各自的标准差均为1.0，由于不同样本量而出现了以下两种情况：

一、当N = 100时，两个均值的联合标准误差 = = 0.14（注2），检验两个均值之差的t = (3.7-3.5)/0.14 = 1.41，其相应的p = 0.160（注3）。

二、当N = 200时，两个均值的联合标准误差 = = 0.10，检验两个均值之差的t = (3.7-3.5)/0.10 = 2.00，其相应的p = 0.047。

可见，随着样本的增大，原来不显著的差别现在显著了，这合理吗？就型一错误而言，完全合理。当N = 100时，如果我们拒绝零假设（即3.7 = 3.5），拒真（“真”= 零假设）的风险由16.0%，太大了，不能容忍；而当N = 200时，拒真的风险降为4.7%，在可以容忍的范围内，所以是合理的。

那么，统计上显著的就一定是实际上重要或有意义的吗？自然不是。问题是我们如何判断一个统计显著的结果是重要或有意义？丁丁想知道的大概就是这种判断根据。这种根据，就是我们说的关系之强度或效应之规模（而不是样本最大量问题）。

判断关系强度或效应规模的一个直观（即非正式）准则是两个均值之差要大于均值的十分之一（注4）。如在本例中，均值之差为0.2、远小于均值的十分之一（0.35或0.37，取决于我们以那个均值为比较基准），显然，即使当N = 200时0.2的差别是统计显著的，但其差别还比较小（相对于均值的取值），没有特别的意义。

判断关系强度或效应规模，还有很多更正式的准则，如Pearson’s r（用于关系强度）或Cohen’s d（用于均值之差，注5），两者还可以互相转换（注6）。在本例中，Cohen’s d = 0.2（注7）。按照Cohen的说法，如果d值小于0.3，效应规模为small（小效应）、如果d值在0.5附近，效应规模为medium（中效应），而如果d值在0.8以上效应规模则为large（大效应）。

我们也可以将d转换成Pearson’s r = 0.1。一般说来，r = 0.1 也是一个弱相关。

下图是对以上讨论的一个小结（包括丁丁问题的反面，即如果统计分析的结果不显著时，大样本有什么好处或坏处）。

 

上图也间接回答了丁丁最后引用的问题“统计学家可以证明任何事吗？”。是的，统计学家可以通过提高样本来拒绝零假设，但是，统计学家无法控制关系的强度或效应的规模。如何提高关系的强度或效应的规模？这既是一个理论问题、也是一个（数据收集）方法问题。本庄以前曾有涉及、日后有机会还会讨论，这里就不扯开去了。

注释：

注1：两者同义。关系强度多半用于相关或回归分析而效应规模多半用于方差分析。

注2：丁丁没有交代是两个独立样本还是两个非独立样本，我们假定是前者。

注3：双尾检验。p值可以根据给定的t值和自由度数，用Excel里的TDIST函数求出。

注4：所以一般说来，做社会科学研究的学生最好分别修一门专讲数据收集方法课和一（至数）门统计课。

注5：, 此外还有其它很多与Cohen’s d大同小异的计算均值之差的效应规模的公式。

注6：

注7：算了老半天，d等于均值之差，这是因为两个组的样本量相等，否则会有所不同或很不相同。

为何两个模型的中介变量系数一样？

tan @ 2009-09-14:

祝老师,您好!这个星期的提问我看您都回答了,除了我提的问题。不知是您没注意到还是问题太初级而不值得回答。由于学识粗浅并确实想知道问题的解答，特此再次提问，烦请老师您或其他有识之人给予解惑。

问题是有关用SEM检验中介效应的：变量W和Z为自变量（且W与Z之间没有显著的相关），Y为因变量，X为设想中的中介变量。首先是模型1，只涉及三条路经：W--X；Z--X；X--Y。所有路经系数都显著，模型的拟合度也可接受；接着是模型2，涉及五条路：W--X；Z--X；X--Y；W--Y；Z--Y，即模型2比模型1多了两条路经（W--Y；Z--Y），结果也是所有路经系数都显著，模型的拟合度也可接受。我不可理解的问题是：在模型1和2中，自变量（W和Z）与中介变量（X）的路经系数竟然一样，怎么会这样？但模型1中X--Y的路经系数要大于模型2中X--Y的路经系数。

在此，我想请教的问题是：（1）上述模型（1和2）中，W和Z与X的路经系数有没有可能一模一样？在理论上成立吗？我担心在那个地方做错了。（2）根据您的几个帖子以及其它相关资料，中介效应并不是比较上述我所表述的两个模型的，但在我所学习的Marketing领域，有文献（作者还有一定的名气）却又是这样做的，特别提到：模型2拟合度可接受，所有路经关系都显著，故部分中介效应显著。这样做可以吗？再次感谢！

庄主 @ 2009-09-20:

上周有好几人提了问题，但我没有时间回答所有人的问题，只能按我对问题价值的判断而选择回答部分。我初看你的问题，觉得与8月31日匿名者提的问题相同（见为何不同模型的路径系数和拟合度相同？）。我现在还是这么认为（即，即使不是同一人问的，道理一样）。考虑到读者中也许还有同样的问题，所以再说几句。

为了便于讨论，我将你的两个模型画了出来（建议：很多时候一图胜千字、但这里的提问处不让上传图像，请大家讲图贴在自己的博客或其它公共空间上，然后在你的问题中做个链接）：

问题一、“上述模型（1和2）中，W和Z与X的路经系数有没有可能一模一样？在理论上成立吗？”是否指λ_xw = λ'_xw和λ_xz = λ'_xz？如是，答案是肯定的。一个回归方程的系数当且仅当方程增减自变量时才可能变化。以本案为例，模型a涉及以下两个方程：

X = λ_xwW + λ_xzZ                           (a1)

Y = β_yxX                                      (a2)

而模型b也涉及两个方程：

X = λ'_xwW + λ'_xzZ                         (b1)

Y = β'_yxX + β'_ywW + β'_yzZ              (b2)

如果比较方程a1与b1，可见两者含有同样的自变量（W和Z），所以λ_xw一定等于λ‘_xw，λ_xz也一定等于λ_xz。（注：这是回归分析的基本原理，同样适用于SEM。）

问题二、“模型1中X--Y的路经系数要大于模型2中X--Y的路经系数”。比较方程a2和b2，可见b2比a2多了两个自变量（W和Z），因此β_yx可能不等于β’_yx，条件是(1)W或Z与Y相关（即β'_yw ≠ 0或β'_yz ≠ 0）和 (2) W或和Z与X相关（即λ‘_xw ≠ 0或λ‘_xz ≠ 0）同时成立。既然现在β_yx > β’_yx，说明W或Z两者之中至少一个与X和Y同时相关。（注：这也是回归分析的基本原理。）

问题三、“模型2拟合度可接受，所有路经关系都显著，故部分中介效应显著。这样做可以吗？”模型b的拟合度一定比模型a好，但是由于损失了2个自由度，所以要做统计检验以证明模型b与模型a之间有显著差别。如是，说明模型b更可取。但是，仅比较模型a和模型b而不比较模型b与只含W->Y和Z->的“直接影响模型”（参见如何检验两个中介变量的效应?），确实不是检验中介效应的充要条件 (necessary and sufficient conditions)。为何你们marketing中有“一定名气”的作者这么做？我无法回答，我只知道科学面前人人平等。包括我在内的很多人都相信David Kenny的检验中介变量方法，不是因为他名气大，而是觉得他说的有道理。

如何分析固定样本数据？

H @ 20009-09-08:

我在分析一个固定样本 (panel sample) 的数据，其中每个人被调查了两次，因变量是定距变量、自变量既有定距也有定类变量。我是第一次做Panel，参考了你在《传播统计学》第15章中“固定样本分析的主要步骤”一节，其中建议当因变量为定距变量、自变量即有定距也有定类变量、数据时点为2时，最简便的是使用回归分析、或者使用协方差分析，其结果应该是完全相同的（第405页）。我尝试了SPSS中GLM模型中的Univariate和Repeated Measures两种方法，以下是我用的指令 (其中Y1和Y2是因变量、X是定距自变量、Z是定类自变量)，

UNIANOVA y2 BY z WITH y1 x/Design.

GLM y1 y2 BY z WITH x/WSFACTOR = y 2 Polynomial/WSDESIGN = y/DESIGN.

发现它们的结果并不相同，不知问题出在哪里？

庄主 @ 2009-09-12:

一、你用的UNIANOVA, 正式名字叫做 ANOVA with lagged dependent variable as a covariate（“含有因变量过去值的协方差分析”，简称ANCOVA，也就是我们书上说的协方差分析）。这种方法，与书上公式15-6的OLS regression with lagged department variable as an independent variable（“含有因变量过去值的经典回归分析”），在数学上完全一样，其结果当然也完全一样（参见前文回归与GLM的分析结果真的不同吗？）。

两者相比，协方差分析在操作上有一个好处：可以直接输入定类自变量，而在做回归分析前，则必须先将定类自变量转换成dummy variables (哑变量)。

不管用协方差还是回归分析，最重要的是要明确被检验的零假设是什么？以本例来说，被检验的是以下的零假设：

1. Y1对Y2没有显著影响；

2. X对Y2没有显著影响；

3. Z对Y2没有显著影响。

注意，因为你用的“DESIGN”指令中没有任何自变量，说明你只想检验Y1、X和Z对Y2的main effects（主影响）而不建议三者之间的交互影响，也许这是你的理论问题所需，当然没有问题，而且也简化了这里的讨论。

从这三个假设来看，假设1只是技术性需要（控制Y1与Y2之间的自相关），虽然绝大多数情形下两者会高度相关，但没有什么理论价值，所以不必介意。假设2和3是核心，分别显示在控制了Y1对Y2的影响之后，X和Z各自对Y2有无显著影响（请记住这句话）。

二、你用的GLM，正式名字是Repeated Measures ANCOVA with two dependent variables （“含有因变量前后测量值的协方差分析”，简称RM-ANCOVA）。这种方法与上述的协方差或回归的不同之处在于其将Y1和Y2同时当做因变量，你将其取名为“Y”（注意，这里的Y是只存在于这个协方差分析之中的一个虚拟变量；并注意这个Y与我们书中405页上公式15-5中的因变量ΔY (= Y2 - Y1) 不是一回事，而是与multilevel（多层分析）第一层分析的思路是一致的）。

我们也来看看这里检验的是哪些零假设：

1. Y1与Y2之间没有显著差别 (即一种Test of Within-subjects Effects)；

2. Y1与Y2之间的差别与X没有显著关系（即Y和X对从Y1到Y2变化的交互影响，也是一种Test of Within-subjects Effects）；

3. Y1与Y2之间的差别与Z没有显著关系（即Y和Z对从Y1到Y2变化的交互影响，也是一种Test of Within-subjects Effects）；

4. X对Y（即Y1和Y2的均值）没有显著影响（这是一种Test of Between-subjects Effects）；

5. Z对Y（即Y1和Y2的均值）没有显著影响（也是一种Test of Between-subjects Effects）。

上述零假设中，1与ANCOVA或回归分析的1相仿，检验自相关而已；4和5的意义不大（因为求Y1和Y2的均值没什么理论意义）；假设2和3也是核心，分别检验了X或Z对从Y1到Y2的变化的影响，与ANCOVA的假设2和3分别检验Y2有所不同：前者是一种Within-subjects Effects (前后变化)，而后者是一种Between-subjects Effects（横向比较）。当然，由于两个模型鉴于同样的数据，所以如果X或Z对Y的前后变化没有显著影响时，其对Y2也不会有显著影响。反之亦然。

两者之间，究竟选用那种模型或报告那种结果，取决于你的研究问题。我个人觉得RM-ANCOVA提供的信息更丰富或更接近一般研究问题，但是其结果的解读更复杂，所以需要有对GLM模型比较深入的理解，否则还是以回归分析或ANCOVA为准。

为何不同模型的路径系数和拟合度相同？

Anonymous @ 2009-08-31：

老师您好! 我也刚开始尝试使用SEM做中介效应分析,看了您的几个相关帖子,受益匪浅。恕我愚钝,还有几个问题不明白,还望进一步指教。

1). 您在"如何检验两个中介变量的效应"的帖子中提到：中介效应需要满足三个或者四个条件,其中包括:X或Z(自变量)对Y(因变量)的间接影响大于其直接影响（即 γAX × βYA > βYX 或 γBZ × βYB > βYZ ）。我不明白为什么一定要满足这个条件？如果是这样，是否意味着中介模型中间接效应都大于直接效应，或者说中介效应的比例大于50%。可我经常看到一些文献说，某某变量的中介效应比例为多少多少（低于50%），难道这是错误？

2). 最近我也做了一个中介效应的模型，概念模型类似于6月30日“如何在模型拟合度和模型合理性之间选择？”帖子中的模型。首先用软件跑了模型1，所有系数都显著，模型的拟合度也可接受；接着跑了模型2，结果是所有路径系数也都显著，模型也可接受。我不理解的问题是：a.两个模型不一样，为什么拟合度都可接受；b.两个模型种，W和Z到X的路径系数尽然完全一样，模型都不一样了，怎么路径系数还会相同？其中，X到Y的系数，模型2要比模型1小？C.模型2中，数据显示 βwx * βxy < βwy ,请问这还存在中介效应吗？

不好意思，一下子问了好多问题，也许许多问题还非常初级，见笑了。不慎感激！

庄主 @ 2009-09-05:

1). 为了理解你的问题，我重读了一项原文，发现其中的直接影响符号写错了（现已改正），应该是γ_YX和γ_YZ或而不应该是β_YX和β_YZ（图中的符号是对的）。也就是说，你问题中提到的为何“γAX × βYA > βYX 或 γBZ × βYB > βYZ” 应该是“γAX × βYA > γYX 或 γBZ × βYB > γYZ"。（当然，你对原文的理解没有错。）

我在原文中说过，严格的中介效应模型要求直接影响（即γYX 或 γYZ）彻底消失。这时，间接影响（γAX × βYA或 γBZ × βYB）自然大于直接影响。如果直接影响不等于0但小于间接影响，那么可以认为这是一种让步或妥协的微弱版（weak version）。如果再推一步，直接影响不但不等于0而且大于间接影响，那么直接影响是主流或中心路径(central route)、间接影响只是支流或边缘路径（peripheral route)，那么中介效应的原始意义就大大打折扣了。这是一个理论问题、不是纯粹的统计问题（意思是，间接影响还存在，但没有必要强调其涉及的“mediation process”了）。

我还没看到过你提到的"中介效应的比例大于50%"，是指间接影响的值至少为直接影响的值的一半吗？如果这样，那是对上述微弱版的进一步弱化。

2a). 你的两个模型不同（模型2多了四个系数、少了四个自由度）、但拟合度都可以接受的现象很正常和普遍，因为各自检验的零假设相同，都是模型与数据之间没有显著差别。但是，你还要检验一个零假设，就是两个模型的拟合度之间没有显著差别：如果两者确无差别（即由于增加了间接影响而提高的误拟合度被损失了的自由度所抵消了），则说明间接影响（即中介效应）并不显著；反之则说明存在显著的间接影响（中介效应）。

2b). 你问“两个模型中，W和Z到X的路径系数尽然完全一样，模型都不一样了，怎么路径系数还会相同？”其中的W从何而来？估计你将我另一帖了的符号（其中也许W和Z是自变量、X是中介变量）混着用了。但是如果是这样的话，X不应出现在模型1.而你却说“X到Y的系数，模型2要比模型1小”相矛盾。难以理解。最简单的方法是提供两个表格，一是模型1的变量及其系数、二是模型2的变量及其系数。

2c). 你问的就是：当一个间接影响小于直接影响时，是否还有必要和价值讨论中介效应？我上面已经讨论过。按经典的定义和学术界的主流看法，至少是意义不大。

如何理解“中介性模型是一个因果模型"?

z @ 2009-08-31:

我的研究假设包含一个中介变量而我的数据来自一次性调查(one-shot survey)，我用SEM分析，结果拟合的很好。但审稿人批评说，虽然模型拟合了，但并没有证明该模型的因果关系，如自变量先于中介变量、中介变量又先于因变量。

我在“中介关系之父”David Kenny的网上(http://davidakenny.net/cm/mediate.htm)读到一句话“a moderational model is a causal model”（“中介性模型是一个因果模型”）。是否可以用来为自己辩护？

庄主 @ 2009-09-05:

恕我直言，你对Kenny的理解，可以说是典型的断章取义。以下是他原话的完整段落：

“Note that a mediational model is a causal model. For example, the mediator is presumed to cause the outcome and not vice versa.  If the presumed model is not correct, the results from the mediational analysis are of little value.  Mediation is not defined statistically; rather statistics can be used to evaluate a presumed mediational model.  The reader should consult the section below on  Specification Error.” （“中介性模型是一个因果模型。例如，假定中介变量影响因变量而不是反过来。如果这种前提假定并不成立，那么中介分析的结果就是毫无价值的。中介影响不能通过统计分析来证明，统计分析只能用来检验以中介性为前提的模型。读者应该参考以下有关模型设定中的错误。”）

相信你一定学过因果关系的三项条件：自变量和因变量之间具有相关性；两者的产生又有先后之别；不存在导致这种因果关系的其它变量。在中介性模型中，这三项条件需要扩展一下：自变量(X)和中介变量(M)之间、中介变量和因变量(Y)之间各有相关性；三者之间的产生又各有先后之别(X->M和M->Y)；不存在导致这种因果链(X->M->Y)关系的其它变量。

Kenny的话指的是在上述条件二存在的前提下，SEM或其它统计分析方法可以检验条件一（甚至条件三，如果你的模型中包括了“一切可能的第三者”）的合理性。如果条件二不存在（如一次性调查数据）的话，拟合得再好的SEM也只证明了X和M之间以及M和Y之间的相关、并没有证明X->M->Y的先后次序。也就是说，哪怕X和M以及M和Y各自高度相关，三者之间的因果链还有X->Y->M、M->X->Y、M->Y->X、Y->M->X、Y->X->M等五种其它可能性！

如果你继续读一下Kenny有关“模型设定中的错误”一节的话，就会知道他在那段的开始还在强调上述（我演绎）的思想：

“Mediation is a hypothesis about a causal network.  …  The conclusions from a mediation analysis are valid only if the causal assumptions are valid.”（“中介影响是一种有关因果网络的假设。 … 中介分析的结论只有在有关因果条件存在之下才能是正确的。”）

还是那句老话，变量之间的因果次序是由数据的采集过程来决定的、而不是由统计分析（包括SEM）来决定的。

如何在EViews或Stata里计算Finsher转化值？

旭 @ 2009-07-23：

祝老师您好！我是一个学经济学的学生，目前正在做毕业论文，是关于跨国GDP与消费之间相互关系的研究。看了您的“如何检验两个相关系数的差别？”一文，感觉受益匪浅，帮助很大。因为这就是我要做的东西：把各国之间GDP与消费增长率的相关系数算出来，然后把对应的GDP与消费增长率的相关系数（如中美之间GDP增长率的相关系数和中美之间消费增长率的相关系数）做费雪转化，求出Z值看他们之间的区别显不显著。在文章里您给出来算费雪Z值的一个EXCEL公式，可以算出结果。但是我的导师说EXCEL不是一个ACCEPTABLE统计软件，让我用EVIEWS或者STATA软件做这个结果，想请教下您，能不能在这两个软件里做上述分析结果呢？如果可以，该怎么做呢？

庄主 @ 2009-08-30:

任何软件只要其公式一样，结果应该是一样的，不存在高贵低贱之分。我曾说过，SPSS是傻瓜机而Excel是智能机，因为前者一般只报告计算结果而不显示计算步骤，而Excel是让你自己一步一步算出结果。就这意义上说，其它统计软件（包括EViews、Stata、SAS等）也是傻瓜机。当然，就本案的如何计算Fisher z-transformation而言，我在原文中教大家的是直接套用Excel提供的函数FISHER()，那也是一个傻瓜工具。但你也可以根据我原文中的公式

 

写出如下的Excel计算公式：=0.5*LN((1+A2)/(1-A2))

注，其中“A2”是你的相关系所在格。你也可以先用函数求、再用手工来验证。难道这样的结果还不acceptable？

如果一定要用高贵的EViews、Stata或其它软件来计算，道理一样。首先，你要建一个新文件，将你的相关系数作为一个变量放到一个column里，然后写一句类似上述Excel公式的指令，如

F = 0.5*LN((1+R)/(1-R))

其中F是转换后的值，R是原始相关系数。我手头没有EViews和Stata的手册，不知它们是有LN还是其它符号来代表自然对数函数。

再次呼吁：同学们大家起来，不要做统计软件的奴隶！

如何解读一个交互影响显著而简单斜率不显著的回归模型？

Anonymous @ 2009-07-30:

Hi, Dr ZHU, I may want introduce myself first, I am a Phd Candidate from your university majoring in xxx (EDITED BY 庄主). I find your forum by accident and I have read some reviews on it, I really feel it is a good place to know more statistics knowledge.

I want to ask one question about the interaction effects of two independent variables (or we may also can say the moderating effect of one independent variable and one moderator, I may name them "A" and "B") on one dependent variable (I may name it "C"). I first use the traditional method, OLS- multiple linear regression in SPSS to run the produced term A*B's effect on C, I got a significant result, the T value is around 2.2 thus the P<0.05.

Then I further explore the internal mechanism of the interaction effect by using Cohen and Cohen (1983), Aiken and West (1991) and Dawson and Richter’s (2006) Simple Slopes Test [this method is designed for interpretation of the interaction effects of two continuous predictor variables, by this way one could interpret the significance level of the causal relationships between independent variable and dependent variable under high or low level of the moderator. To illustrate and test the significant interaction effects, separate regression lines were computed, plotted, and tested with one standard deviation below the mean on the moderating variables as well as one standard deviation above the mean of them.], this time I find the causal relationship between A and C is insignificant both under high B and low B level, in fact the coefficients take the opposite direction. Under high B level the coefficient between A and C is negative but insignificant, under low B level the coefficient between A and C is positive but insignificant.

I originally explain the significant moderating effect is: although under both high and low B level the causal relationship between A and C is insignificant, but because of the opposite coefficient, thus the moderating effect (A*B) may still be significant. But current one famous professor rejected my explanation; he told me that the results were inconsistent: 1. from one side, the moderating effect is insignificant. 2. form the other side, both under high and low B level, the causal relationship between A and C is insignificant thus can be treated as no relationship. How can you say them taking moderating effect first and later told us the effects were equal (A and C have no relationship) under both conditions (high and low B level)? Thus I am a little confused, as you know, in many cases, run the linear regression will meet such question as I described, so commonly how can we explain this phenomenon to cope with the journal reviewers' critique on this issue?

Many thanks!

庄主 @ 2009-08-29:

Thanks for the detailed explanations of your question.  It’s satisfying to know that someone of my own institution also reads this blog. Sorry for the delayed response as I’ve been traveling in the summer. To benefit other readers who might not be efficient in English, please allow me to reply in Chinese.

先简单回顾一下你的问题。你有模型1

C = b₀ + b₁A + b₂B + b₃AB                       (1)

其中A、B和C都是定距变量。你用OLS回归检验，发现b₃（还是b₁或b₂？）的t值 = 2.2 (p < 0.05)，即AB对C有显著的交互影响。为了进一步理解这种交互关系的“内在机制”，你采用了Cohen & Cohen等推荐的“简单斜率检验法”(test of simple regression slope)，即根据模型1的结果，将B的均值±1个标准差的值（分别记为B_H和B_L）代人模型1，来算出以下两个简单回归模型的斜率：

C = b₀ + b₁A + b₂B_L+ b₃AB_L = (b₀ + b₂B_L) + (b₁+ b₃B_L)A             (2)

和

C = b₀ + b₁A + b₂B_H+ b₃AB_H = (b₀ + b₂B_H) + (b₁+ b₃B_H)A           (3)

说明：因为B_H和B_L均是一个常数（而原来的B是一个变量），所以它们代入模型1后而得到的模型2和3，经过整理以后，都成为只含自变量A的一元（或简单）回归模型，而模型2中的b₁+ b₃B_L和模型3中的b₁+ b₃B_H就是你说的的简单斜率（就是我用蓝色标明的部分）。这时，你发现模型2的简单斜率b₁+ b₃B_L成了负值而模型3的简单斜率b₁+ b₃B_H仍是正值。你进一步对这两个斜率作了显著检验，发现两者均不显著。你的结论是“虽然A在调节变量B的不同条件下对C都没有显著影响，但是A和B的显著交互影响仍然存在”。但是，一位著名教授不同意你的说法，理由是：一、你的交互影响不显著（我不理解这句话，因为它与你说的模型1中的t = 2.2有矛盾）；二、A在B的不同条件下对C的影响都不显著。（不知我的上述理解是否有误？）

好了，现在谈谈我的看法。

首先，我有两处不清楚：一、如我已在上面问过，模型1中显著的是b₃还是其它系数？二、你还没有提到，模型1中的A、B和AB是否为各自的centered values（“取中值”，以避免或降低AB与A、AB与C之间的相关程度）？鉴于你已读过Cohen & Cohen, Aiken & West等经典文献，应该熟悉检验交互影响的基本步骤，所以我的回答是基于以下假定的：一、你说的模型1中t = 2.2的显著系数是b₃；二、模型1中AB与A、AB与C之间并不相关（这点很重要，不然、假定一是没有意义的）。

如果上述两个条件成立，那么你的A和B在样本中对C就是确实具有显著的交互影响。当然，因为你的t值接近临界值（1.96或更大），AB的交互影响应该是marginal（相当勉强）的，所以要审慎对待，至少要检查一下A的数据中是否存在异常值；如有异常值，则需要剔除后再次检验模型1，看看AB的影响是否继续保持显著，已确保该模型的robustness（“鲁棒性”）。

你的主要困惑（也是你教授理由之二）在于：为什么在模型1的b₃显著的前提之下，模型2和3的斜率不显著？这里存在一个许多教科书上没有明确解释、但初学者往往容易误解的事实，即AB之间的显著交互关系只是说明自变量(A)对因变量(C)的主影响(main effects)将随着调节变量(B)的取值而变化，但并不保证在B的不同取值上A的所有主影响都是显著的（但至少有一个取值上A的主影响是显著的，否则AB不可能显著）。用英语说，A significant interaction effect ensures not only the main effect of an independent variable on a dependent variable varies across different levels of a moderator variable, but also at least one of the main effects is significantly different from zero. However, the significant interaction doesn’t guarantee all main effects of the independent variable on the dependent variable to differ significantly from zero. 我们很容易用以下的图示来说明这个道理。

左图是我随手画的，其中有五条回归线，但都是根据同一模型（如你的模型1）而取B的最大值(Max)、最小值(Min)、均值(Mean)、均值减一个标准差（你的模型2）、均值加一个标准差（你的模型3）而画出的。虽然没有实际数据，但可以大致猜出五条回归线所依据的模型1的b₁和b₃的取值范围，即b₁（即A的总斜率）应该等于0，b₃（即AB的交互影响）则明显大于0（因为A对C的影响是放射的、即随着B的增加而增加）。当然，我们并不知道（也无必要知道）b₀和b₂的取值范围，因为它们与本案毫无关系。

图中B=均值的回归线显然是一条水平线，所以是不显著的(即斜率等于0)。而B=均值加/减标准差的两条线，虽然并非水平线，但也很接近，考虑到各自的抽样误差（注意，不要与标准差相混淆了）而其斜率与0没有显著差别（也许你的数据就是这种情况）。但是，B=极大值/极小值的两条线的斜率显然不等于0。如果我们再添加B=均值+/-2个标准差的两条线，可以想象它们的斜率也会不等于0。结论：当A和B对C有显著影响时，A对C的影响随着在B的取值而变化，有些显著而有些可能不显著。

以上是直观的解释。我们还需要略正规一点地总结一下。回到模型2和3，注意其中的蓝色部分（即各自的斜率）。它们是否=0，是由下述公式来检验的：

 

 

和

其中Var_b1和Var_b2分别是b₁和₂的方差、Cov_b1b3是b₁和₂的协方差。我们略过如何计算系数的方差和协方差的技术细节，而来看一下如何使得t_L和t_H达到显著水平（即大于2）。不言而喻的是分子要大而分母要小。就分子而言，从表面上看b₁、b₃和B_H或B_L三者均要越大越好，但更重要的是要三者取同样方向，否则会互相抵消（这不容易做到，尤其是当数据经过中心化处理之后，B_L一定是负的，而b₁或b₃的方向也会因A或B的中心化而与原始数据的方向相反）。而且，调节变量的取值(B_L或B_H)也不是越大越好，因为同时也会扩大分母。结论：t_L和t_H的取值受到很多正反因素的影响，很难做到永远显著。但是，这与b₁是否显著没有一一对应关系。

最后，你问如何使得期刊的reviewers接受你的解释。是的，有些（如果我用“很多”的话，大家可能会觉得我太狂妄，但是事实上“有些”不是一个小数目）reviewers也会将交互影响等同于主影响，所以你不仅要自己弄得很清楚，而且要说得很明白易懂，这时，公式和图表就是必要的辅助工具了。如何写好交互影响的报告，确是一个挑战。多读几遍Cohen & Cohen吧（他们的第三版就邀Aiken和West加盟合写了）。

给SSCI期刊投稿应该先投后改还是先改后投？

P @ 2009-08-20:

您怎么看下面两位SCI/SSCI期刊审稿人的对话？有人也建议过我先送出去审，拿到意见再修改。

甲：投稿又撤稿，特别是给出修改建议之后再撤稿，有点不厚道。我遇到很多次，写的审稿意见不比文章短，从字词到如何布局，那些内容如何做，都写到审稿意见里。善意地给了revise & resubmit的意见。实际上，按照标准，reject一句话就是了。可是，过几个月后发现发表在另外一个杂志上。这种做法可以理解，但是不厚道，至少应该想办法感谢审稿人。

乙：我审稿也通常善意地给revise & resubmit的意见，很累，有些投稿者把审稿人当成论文加工把关人，不厚道。于是也慢慢的拒绝审一些稿件，或者直接reject。

庄主 @ 2009-08-22：

我看了之后的第一个感觉就是我们有些同胞真聪明，知道如何玩这个游戏！但是事实上，将草草急就章的文章投出去，往往拿不到什么真正有价值的反馈。上面乙某说的就是一例。我亦是如此。刚开始做审稿人时，不分良莠，每篇文章都写较详尽的修改意见。记得最多一次密密麻麻用单行写了5页，应该有3000字吧（但跟别人相比，还不算很长，下面引述的研究中最长的意见有6000多字呢）。但后来慢慢地就变得区别对待了，仍然愿意给“好”文章（不仅理论和方法好，而且写得通顺）提建设性意见、而对“差”文章（或者理论/方法差，或者写作差、包括完全不顾APA style规则的，），则草草几句“锯”了。

前不久读了Russell Neuman等人在JOC上发表的“传播研究中的七宗罪”一文，得知上述乙某和我的做法确实是大部分审稿人的习惯。Newman等分析了JOC的审稿人给100余篇投稿（包括采纳和拒绝的）写的具体意见，其中表四（见左）的数据展现的是审稿人对每篇来稿定的“罪名”数目。粗粗一看，被拒绝的稿件（白条）的罪名数少于被发表的稿件（黑条），如被发表的文章每篇平均有16条“表述不清”的罪名而被拒绝的文章每篇则有7条此类罪名。但是，这并不说明被拒的文章写得更好。恰恰相反，那些文字是too bad to be rescued（朽木不可雕），审稿人懒得多费心思。

Neuman等还做了一个多元回归分析，发现审稿人给每篇投稿写的意见长短是预测该文是否被采纳的重要指标之一。具体而言，意见每多1000字，有关文章的发表率就提高9%！所以，当你收到投稿的反馈时，如果是数十的批评，应该暗暗庆幸，该文很有希望。

以下是Neuman等的原文(下划线是我加的)：

“We find a dramatically larger number of negative comments on average for accepted papers, especially on the dimensions of clarity, methodology, and completeness. On closer examination, it turns out to make sense in terms of the psychology of the hard-working volunteers called upon to provide the reviews. If the overall importance and theoretical integration of a submission is weak, the reviewers simply do not bother to spend a lot of time with constructive but negative comments on such things as clarifying an argument and strengthening the methodological presentation. On papers likely to be published, reviewers may go to greater length to indicate how the authors might be more complete and clear in their presentation.” (p. 229)

“This appears to be the academic journal review equivalent to the hoped-for thick envelope from a favored college to which one has applied—the more the reviewers say, positive and negative, the more interest in the submitted paper. So we examined the cross-tabulation of the total number of reviewer words and the likelihood of publication and ran a rudimentary linear least squares and determined that roughly for every additional 1,000 words of reviewer comments (including all dimensions), one’s chance of acceptance increases approximately 9%.” (p. 229).

Reference

Neuman, W. R., Davidson, W., Joo, S. H., Park, Y. J., & Williams, A. E. (2008). The seven deadly sins of communication research. Journal of Communication, 58, 220–237.

如何解读这个调查报告？

ANY @ 2009-08-19:

今年XX单位做了一个YY方面的调查，报告出炉后争议很大。我呢，虽没参与争议之中，因专业之故，很是关注。就我个人意见，我非常不理研究者组使用RDD法抽取了647人来代表全体北京人口，给各媒体排名。我极其质疑它使用的抽样技术。我认为非概率抽样中的配额抽样可能更适合做这个调查。

庄主 @ 2009-08-20 答: 我没看到那个报告。请进一步说明清楚，你质疑的是样本量太小、还是RDD（随机电话号码抽样）原则、或者其它问题？

你建议用配额抽样，我可以肯定地说配额抽样一定不适合。

ANY问：

我首先质疑的是调查组的抽样方法。我和研究者联系，希望得到更多细节，比如是随机拨号法，还是集群拨号法，但无法得到。 刚巧收到了回复，说：“抽样方法采用的是RDD，先通过不等概抽样（pps）确定前面四位局号，后面四位是随机选号（北京电话号码是8位），抽样是座机。”在此之前的争议中，有人怀疑的是647个样本来代表2000多万北京人的代表性。

庄主答：

你的怀疑和批判精神值得提倡。当然，如果对抽样基本原理有比较清楚的理解，则可以避免在怀疑和批判时犯常识性错误。

第一、样本大小涉及的是调查结果的精确度问题、而与代表性无关。样本越大、结果越精确，反之亦然。精确度有公式可以计算，即抽样误差。当N = 647而可信度 = 95%时，抽样误差 = ±3.8%。这个精确度是否足够？答案取决于具体的研究问题。如果被排序的两个媒体之间相差8%或更大，那么它们的高低是可靠的；反之则不然。

第二、抽样误差与总体大小无关。所以无论北京人口是2千万还是2亿，样本为647的抽样误差大小是不变的。

第三、样本的代表性取决于抽样是否随机、而与样本大小无关。如果一个非随机样本N=10000，虽然其抽样误差 < ±1.0%，但仍然没有代表性。一个没有代表性的大样本比一个精确度低的小样本更无价值。

ANY问：如果是抽取座机号码的话，我现在也高度怀疑样本的代表性。因为有很多在北京的人，终其一生不用座机。据经验推测的话，许多有北京户口的人也不见得使用座机。而上一次人口普查是把大量北漂计入了北京人口的。把大量无座机电话的人排除在总体之外，这意味着什么呢？而这是为什么我觉得配额抽样更好的缘故。

庄主答：

同意。如果上述调查的RDD是严格执行的话，那么其代表的是北京有座机的家庭人口。也就是说，该调查的Study Population（研究总体）是北京有座机的家庭人口、而不是北京所有家庭人口。研究者在报告时应该说明这一点。当然，研究总体限于“北京有座机的家庭人口”的一个调查是否有价值，即取决于其与北京所有家庭人口之比（你知道到底有多少人被排除之外的吗？）、也取决于研究目的。如果有关媒体（或广告商）更关心有座机家庭人口，那么也是无可非议的。商业调查毕竟不是民意测量。

配额抽样不是随机抽样，调查结果毫无价值。现在考考你：为什么配额不是随机抽样？

ANY问：

研究者用盖洛普1932年用1000个样本代表美国人预测了总统选举来证明其647人样本有代表性。我觉得这是个外行的支持。

庄主答：

你觉得我上面的回答是否已经解决了这个问题？如无，我再啰嗦几句。

ANY问：

问卷是看不到的。我个人看法，即使是RDD法，考虑分众化和个人媒介使用的多样性，问卷设计应当是一套很复杂的问卷。

庄主答：

抽样、问卷设计和调查（即问答过程）代表了每项调查的三个主要误差来源：抽样误差、工具误差和测量误差。每一项都要小心处理，并应在报告（或技术附件中）详细透露。如抽样方法、问卷原文、调查过程（尤其是最后一步的个人是如何被抽取的），以便读者对其研究结果的质量作出自己的判断。

ANY问：

我的问题纯出于专业上的兴趣。我非常想弄清楚这个问题。再次感谢您！

庄主答：

我是出于同样的原因而回答你的问题。

如何在SPSS里删除重复ID的个案？

L @ 2009-08-01:

如果在SPSS数据库里有一个变量是对case的编号，现在有可能某些case 是重复出现的，我想要将重复出现的case只保留一个，其余重复则删除掉，怎么完成这个任务？(除了手动的以外。）

庄主 @ 2009-08-02:

SPSS13版或之后的Data菜单下有一个“Identifying Duplicate Cases”的程序，应该可以解决你的问题。但我没有用过那个程序，而是用下述的syntax写一个程序来做，自己写的程序放心一点，不会错杀无辜的个案。（注：以下syntax其中的“ROW”和“ROW2”是两个临时变量，事后可以删去。如果你case的编号变量名不叫“ID”，请修改ID。）

sort cases by ID.
compute ROW=$casenum.
aggregate outfile 'c:\temp.sav'/break ID/ROW2=first(ROW).
match files file */table 'c:\temp.sav'/by ID.
select if ROW=ROW2.
delete variable ROW ROW2.
exe.

强烈建议你运行前，请先用下述模拟数据试一下，以检验上述程序是否对（即没有放过任何需要删的个案、也没有错删任何需要保留的个案）。

input program.
loop #i=1 to 10.
loop #j=1 to 3.
compute ID=#i.
end case.
end loop.
end loop.
end file.
end input program.
sort cases by ID.
compute ROW=$casenum.
aggregate outfile 'c:\temp.sav'/break ID/ROW2=first(ROW).
match files file */table 'c:\temp.sav'/by ID.
select if ROW=ROW2.
delete variable ROW ROW2.
exe.

数据a	数据b	数据c	数据d

上述syntax的第1-11句生成一个含有两个变量（ID和ROW）、30个个案（其中仅10个独立个案，但每个个案重复3次）的数据（见下图数据a）。第12句将数据a中每三个重复个案中的第一条记录的ID和行序号ROW抽出来保存到临时文件temp.sav中（见数据b）。第13句将数据a和数据b合并成数据c。第14句将数据c中的ROW（即数据a中的行序号）与ROW2（即数据b中的每个个案第一行的行序号）相等者选出；也就是说，将ROW和ROW2不相等者（即每个个案的重复行）删除。最后，第15句将临时变量ROW和ROW2删除，结果就是你想要的数据d。

为何回归系数这么小?

Anonymous @ 2009-07-15:

我在做一个简单的多因素回归，96个cases, 13 个自变量。 回归结果显示全部coefficients 小于0.005， 其中部分变量p值显著。为什么会这样？这个结果该如何改善或解释呢？急，多谢！

庄主 @ 2009-07-19:

这个问题的答案较简单。如果你说是非标准化回归系数，则反映出你的自变量取值很大或因变量取值很小；如果你说的是标准化回归系数，则反映出你的样本很大（但实际上你的n = 96）或自变量之间有共线性。这两种情况的本质不同，需要分别简述。

非标准化系数

其定义为 the exact amount of change in the dependent variable as the independent variable goes up by one unit when other independent variables are held constant（恕我不翻，我觉得任何中译都不够原文明了精确）。这里的"exact amount of change”的单位，是由自变量和因变量的测量单位决定。假定你的一个自变量自变量是年龄，而因变量是身高，样本为青少年（12-17岁），如果年龄以年为单位，身高以厘米为单位，非标准化系数 =  10，则说明在这段年龄中，每增加1岁，身高长10公分。但是如果年龄以天为单位，其非标准化系数则 = 0.027（=10/365）。相反，如果年龄以岁为单位，身高以毫米为单位，其系数 = 100 (=10x10)，等等。你可以变换两者的各种取值单位，可以得到小到5-6位小数、大到5-6位整数的系数，但其相关程度永远是一样的。希望你能够因此而举一反三，得出如果解释你的结果之方法。

标准化系数

其定义为the exact amount of change in the standardized dependent variable as the independent variable goes up by one standardized unit when other independent variables are held constant（只是多了standardized一词）。这时，无论自变量或因变量取何单位，其系数的值不会变化。如果标准化系数 = 0.005，反映的则是一种很弱的相关关系。为什么还会显著？上面已提到，原因一为样本（巨）大，这时该关系虽然有统计显著意义、但缺乏实际（即理论）意义；原因二是（部分）自变量之间高度相关，导致（部分）系数的标准误差人为变小而达到统计显著，这种结果更有误导之效。你的数据是小样本而多变量，更容易发生第二种情况。一般说来，每个自变量需要有30左右的个案。你有13个自变量，需要400个案。如果只有96个案，则只能用3个左右变量（可以讲高度相关的自变量组成因子来减少自变量个数）。

如何在模型拟合度和模型合理性之间选择？

hz @ 2009-06-25: 我对四个变量之间的关系做了SEM检验，从拟合指数看第一个模型略优于第二个模型；两个模型路径系数显著性如图所示，实线代表通过显著检验，虚线代表没有。你觉得四个变量之间的关系应该如何解释比较好？

庄主 @ 2009-06-30:

从逻辑上说，模型2是合理的、而模型1是有问题的，因为模型1没有检验W和Z对YL的直接影响，而只是假定X是前两者的中介变量。

从实证结果（比较模型1和模型2）来看，Z对Y有直接影响、而X即不是一个中介变量、甚至也不是一个对Y有影响的自变量。这些发现，说明模型1中的X -> Y的显著影响其实是一个由于遗落了Z这个“第三者”而造成的 spurious（虚假）关系。

你提到，模型2的拟合度不如模型1。这是因为模型2比模型1多用了2个自由度。如果去掉W –> Y 和X –>Y这两对不显著的关系之后，两个模型的拟合度应该相似。但是，其实没有必要节省这2个自由度。如果少了2个自由度而使得原先可以拟合（即p > 0.05）的模型变成不可拟合（p < 0.05），说明你的样本太小，原先可以拟合的模型也是在边缘线上挣扎。

我们检验模型拟合度的目的是看该理论模型与实证数据之间的差别是否小到可以接受的程度、而不是追求模型的最佳拟合度。其实后者很容易通过其它不值得提倡的方法来做到（参见我前些日子的有关帖子）。

如何在SEM中处理dummy变量和显示R平方？

月出 @ 2009-06-09:

祝老师,您好!您的伯克真的很好，blogspot我一直登不上。我初学LISREL，有几个问题想请教您：

1、虚拟变量在SEM中一样用0、1处理吗？我在原先运行得出的模型里加入了性别变量，但就显示

W_A_R_N_I_N_G: PHI is not positive definite
W_A_R_N_I_N_G: PSI is not positive definite
W_A_R_N_I_N_G: The solution was found non-admissible after  50 iterations. The following solution is preliminary and is provided only for the purpose of tracing the source of the problem. Setting AD> 50 or AD=OFF may solve the problem. 这是怎么回事?

2、子模型原先得出的变量之间的关系为什么进入母模型后显著性发生变化？路径系数的正负也反了？正常吗？怎么解释？比方说总风险和各类风险之间本来是这么个关系,加入信任置于总风险前，总风险和各类风险之间的关系就变化了。可能有什么问题存在吗？

3、我怎么在LISREL中显示可决系数R平方阿?

庄主 @ 2009-06-27:

1、SEM中可以包括虚拟变量（dummy variables）。一般是先用LISREL中的PRELIS工具将含虚拟变量的相关系数矩阵转化成tetrachoric correlation矩阵（参见http://ourworld.compuserve.com/homepages/jsuebersax/tetra.htm），然后再进行分析。

你得到的出错信息由很多种原因造成，可能是你模型的设置有问题（如性别要factor loading = 1、factory error = 0）、也许是性别与某些其它观测变量之间的高度相关、等等，很难一下子知道是什么原因。如果用了上述转化矩阵，仍有类似问题，那么更有可能是模型设置的问题。

2、子模型的关系进入母模型之后显著性出现变化是常见的、但是如果系数方向也反了，说明母模型中含有一个disorter的第三者变量（具体参见我前些日子的有关帖子）。你也可以将先后两个模型的系数用表格的形式贴出来给大家看看。

3、LISREL将R平方叫做 Sqaured Multiple Correlations (SMC)。如果你是用SIMPLIS，需要加一句“LISREL OUTPUT EF“ 来显示。需要尤其注意的是，LISRE同时给出计算Structural Form 和 Reduced Form两种结果，前者中的SMC是错的，要看后者。（具体参见Joreskog的文章 What is the interpretation of R2?)

如何处理Power-law(幂率)分布的数据？

Anonymous @ 2009-06-11:

祝老师：您好！看了您关于“如何在SPSS中做数据正态转化”的帖子受益匪浅。 我做的研究是关于web 2.0 的，所以数据来源都是secondary source，有很多变量的分布都是power law的形式，其中有的自变量数据有点类似count variable（0值有意义，非missing value）占了很大的比例。想就数据转化继续请教您两个问题：

1。比如两个自变量IV1和IV2都是高度偏态，在对其进行对数变换后转化为正态。但是IV1和IV2可能对因变量DV存在交互影响， 那么在检测交互影响的时候interaction term是应该用lnIV1*lnIV2么？因为这里有个疑问是lnIV1+lnIV2=ln（IV1*IV2），如果lnIV1和lnIV2进入后R Squared Change显著的话是不是就代表已经存在交互影响了么？还需要继续进入lnIV1*lnIV2么？对这个问题我感觉有点钻到牛角尖里了，想了很久都不太清楚？

2。另外是关于前面0值太多的自变量 （单峰非正态），有点类似于medical research里面的account variable，0代表没发生，但他们是自变量，而不是因变量， 所以感觉不能用Logistic回归。 我试着用了log之类的转换， 很难变成正态分布，目前我将其转换成了dummy variable 0 和1做了一个model，然后再选择所有不为0的obsevation做了一个model，但这样做得结果不是很理想。请问是否有一些特殊转换处理这方面的数据呢？

庄主 @ 2009-06-20:

问题一较简单：交互影响模型中的自变量是否可以取对数？答案是肯定的。因为在你的模型 Y = b0 + b1ln(IV1) + b2ln(IV2) + b3ln(IV1)ln(IV2) 中的右边前两项，即IV1和IV2各有一个回归系数b1和b2，所以它们不会被约简为另一个b3ln(IV1)ln(IV2) 。

同理，模型右边第三项 b3ln(IV1)ln(IV2) 简约后成为 b3 (IV1 + IV2)，也不等同于前两项 b1ln(IV1) + b2ln(IV2)。当然，第三项的变量 (IV1 + IV2 中的联合分布比IV1和IV2原先的独立分布更加不对称，即更加偏离正态分布。但是，据我的理解，当你将 ln(IV1)ln(IV2) 输入OLS回归时，计算程序是将 ln(IV1)ln(IV2) 当做一个值处理而不会将它分析成IV1 + IV2的。

问题二很复杂：如何处理服从power-law（幂律）分布的数据？这种分布特征的数据，具有很多个最小值、而这些最小值由于受到某种机制的限制而无法再往更小的方向延伸（left-censored），而全部堆积在一起。也有人称其为 "floor effects” （“地板效应”）数据（如下图a）。初看，这些最小值（本例是1）堆起来不像是地板效应、而像 “ceiling effects”（“天花板”效应）。但如果将图a作90度旋转，就可以理解“地板”的意思。当然，这种分布的反面，即一组数据中有很多个无法更大的最大值（right-censored values），就是“天花板”了。

以上图a中的X，按三个不同的幂律值（1、2、4）而形成三种不同的“地板”分布（即P(X)=X^-1、P(X)=X^-2、和P(X)=X^-4。具体说来，当幂律=-1时，X的最小值占了总体的19%；当幂律=-2时，X的最小值占了总体的61%；而当当幂律=-3时，X的最小值占了总体的92%！在经典的“正态分布世界”(the world of normal distribution) 里，我们都是用log来转换服从幂律分布的数据。以下图b就是对图a中的三组X用log转换以后的分布形状：

与图a相比，图b中的三种分布的形状不那么“地板”了，但是还远远不是正态分布的。如果将X的频数（即P(X)）也作log转换，即得到一个单调递减的线性分布（图c）：

图c也不是正态分布。但在“正态世界”里，线性分布是我们对付幂律数据的（相对）最好方法了；就是说，幂律分布的数据永远不可能转换为正态的。真的没有其它方法了吗？有，那就要离开正态世界而进入“变态世界”(the world of abnormality)、做一个研究“变态行为”的“变态学者”。“变态”这个字太刺眼。做“变态研究”的绝大多数是拘谨的物理学家，当然无法承受世俗的歧视，所以将变态世界叫做“复杂系统”(complex system)。我一开始说“这个问题很复杂”，意思就是“这是一个复杂世界的问题”。当然，复杂系统也不能点石为金，将幂律分布数据变成正态分布数据、而是用整个一套完全不同的思想和方法来看变量的分布和变量之间的关系。(参见A. Clauset, C.R. Shalizi, and M.E.J. Newman, "Power-law distributions in empirical data" SIAM Review, 2009)。

好了，别再继续问我变态世界的事，我刚刚开始接触他们的那些事，可能受正态世界的毒害太深，无论理智上或感情上都还没有入门。

回到你的实际问题，你可以试试以下几种方法：一、对X取log之后、再取log（当然，如果log(X)有非正值、需要先对其做线性转换成正值）；二、将X转换成0-1值的dummy variable后直接进入模型（而不是用来分拆成两个模型）；三、将X与其他相关的自变量合成新的变量；等等。注意，上述任何一种方法都不会产生正态分布、所以其结果都是差强人意的。

如何设计博士生学习计划？

W @ 2009-06-13:

我是学习传播理论方向的博士生，有志于从事科研，但非常担心自己把博士读成了“5年制的硕士研究生”，于是想做一个合理的读博计划，特别想听听您的建议与看法。我的问题如下：

1、读博期间应该定一个怎样的目标？

2、如何突破研究方法的局限和英语的缺陷？

3、如何培养捕捉一个有创新意义的研究课题的能力？

4、如果方便，很想知道您是如何度过博士生活的。

5、香港的传播学博士是如何读的，您一般对他们有何要求。

6、请您帮我推荐几本您认为应该读的书。

庄主@ 2009-06-14：

你的绸缪未雨想法很好。“博士生=五年制的硕士生”一说我还是第一次听到，但仔细想想，好像很深刻、有道理。同理，硕士生要防止做“六年制的本科生”。也许博士生还要防止做“九年制的本科生”。（申明：我没有任何贬低本科生的意思。事实上，包括我在内的很多海外教授，认为中国本科生的基础训练是非常好的，所以大家更喜欢招中国本科生做博士生。）

你的六个问题涉及了博士生学习的各个方面，我都没有“权威”的答案，但愿意分享自己的体会。由于时间限制，我先简单谈谈，希望各位（包括我在的学生，其实以下很多是以他们作为对象而写的）补充和辩论。

1、目标：扎实基础、广博知识之类笼统的话，我就不说了。我的基本原则：目标一定要高，取法乎上、得乎其中嘛。同时要可操作，如以下两条：一、能教三门课（分别为理论、方法和应用。应用课可以是采编写、也可以是广告策略、公关写作、网页设计、视频编辑，等等，至少能教其中之一。我最近几年每年教的课里，就有理论、方法和网页设计）；二、在高水平期刊上发表一两篇论文（如SSCI中JMCQ或更好的期刊，国内期刊则要比《新闻与传播》等更有挑战性的）。

2、方法与英语的局限：一语以蔽之，只有多动手练习。方法上，对初学者来说，一定要严格遵循规则、步骤、要求，不要马虎、妥协、变通，否则不如不学。英语，对国内学生来说，标准是能写出别人看得懂的论文。最大的敌人是自己（Chinglish、汉式英文）。如何克服？找个native sepaker批改你的几篇文章，然后从中找出自己问题的规律，贴在墙上天天看。

3、创新能力：除了经验，好像没有捷径。而经验来自年份。我的体会是进入学术圈（不一定是从博士生开始）后，努力工作十年后才会发生。自然科学研究也许不需要这么长的周期。社会科学中除了少数天才之外，很少有在博士生期间、甚至在毕业后几年内有真正的重大创新。所以我不把创新当做自己读博士时的目标、也不以它来要求我的学生。

4、我的博士生活：与其他留美博士生一样，大部分时间在上课。我在三年八个学期（包括两个暑期）中大概修了20门课、另外旁听了4、5门课。然后通过四门资格考试（基础、方法、两个专业方向）。最后写论文（那倒是最省时的，只花了半年）。事后觉得收获最大的一是方法训练、二是英文写作、三是体验老师们的人格魅力（不通人情的认真、自我贬低的幽默感、平民的心态、凡事先质疑的精神、等等）。其它的，如看了无数的文献等，在有了wikipedia和youtube的今天，都算不了什么。

5、我对自己博士生的要求：以前我是沿用美国老师教我的方法，即除了学校（和市场）的要求之外，从来没有其它特别的要求。学校的要求是最低限度的，保证能够毕业。市场（用人单位）的要求，对学生来说是看不见摸不着的。最近（在你来信之前），我已开始反思这种hands-off传统的优缺点，并计划从今年开始，给新生提些具体要求，目前想到的就是目标里的三门课、一两篇论文。当然这些只是建议，即使做不到，照样可以毕业，但很难被市场认可。

6、推荐书：以下是对国内新闻传播学博士生的建议（日后也许会有补充）：

方法：

1. Earl Babbie: The practice of social research, 11th ed. (清华影印版)
2. Publication Manual of the American Psychological Association, 5th ed. (俗称APA Style，尽量不要看中译本）
3. Jacob Cohen & Patricia (2002). Applied multiple regression/correlation analysis for the behavioral sciences, 3rd ed., (books.google.com上有免费的部分章节；或其它类似统计书，第一本看原版、也许可以接着看我们的传播统计学。)

理论：

1. Denis McQuail & Sven WIndahl (1993). Communication models for the study of mass communication, 2^nd ed. (同样，先看原版，也许可以接着看我的翻译本).
2. Werner J. Severin & James W. Tankard, Jr. (2001). Communication theories: Origins, methods, and uses in the mass media, 5th ed. (不要看中译本）
3. 新闻传播学实证研究的经典报告（可参见我的传播原理课程的补充阅读目录）

如何处理和解读三角关系中的扭曲变量(distorter)?

龙猫 @ 2009-06-08:

庄主好，日前在研究中遇到一难题，想请您赐教。自变量ABCD通过中介变量E影响因变量F，但加入自变量G后导致E到F的路径系数由原来的显著正相关变成了负值，不知如何解释和处理？我自己的推断是G变量对F变量的解释力过强，压制了E变量对F变量的影响，但我不确定这样推理对不对。另外，也不知如何处理这类问题。故在此请教庄主，谢谢您。（注：研究的样本量为320，
测题数目为30.）

庄主 @ 2009-06-13:

为了便于其他读者的理解，我根据你的叙述，将你的两个模型分别复原在图1a和图1b中（注：图b中红线部分为我所加）。由于你没有说明G与A-D的关系，我假定G不是从A-D到E的另一个中介变量（如果是，问题会更复杂一些）。也因为如此，你的问题其实只涉及E、F、G的三角关系，与所以我加了一个红框，以下来集中讨论三角关系中可能出现的各种问题。

再重复一下你的发现：在没有控制G之前，b_FE是正值；而引入G之后，b’_FE（注意b的上标中的“’”记号）成了负值。你认为G是一个压抑变量（suppressor），不知如何处理G。

先讲讲三角关系的基本原理：

1. 一个第三者（G）当且仅当同时满足以下两种条件时，才会改变原有自变量（E）和因变量（F）的关系：一是G与E相关、二是G与F相关。（你的数据看来同时满足了这两条。）
2. 所谓“改变原有关系”，包括了三种不同的变化：一是改变了significance of the relationship（显著水平，即b值从不显著变显著或反之）；二是改变了strength of the relationship（强度，即b值从小变大或反之）；三是改变了direction of the relationship（方向，即b值从正变负或反之）。注意：这三种变化不是互斥而是独立的，即三者中的任何组合都可能同时发生。（你只说了你的数据中出现了方向的变化，不知原有关系的显著水平或强度是否也有变化？）
3. 所有上述三种情况的变化，都说明E和F的原有关系是spurious（虚假）、靠不住，而引入第三者G是必要和合适的。（即你的模型a是错的而模型b是对的，应该接受后者，哪怕后者否定了你原先的假设。其实，对有经验的研究者来说，后者的出现更令人振奋，因为突破也许就在其中！）
4. 第三者的角色，根据上述不同变化而分为distorter（扭曲变量）和suppressor（压抑变量）两种，当然也可能是两者兼顾（详见下表）。简单说来，扭曲变量的缺失导致了Type I的错误（如不应该显著的成了显著、微弱关系的成了强势关系、正的关系成了负的、负的成了正的，等等）；而压抑变量的缺失则导致了Type II的错误（如应该显著的成了不显著、强关系的成了弱关系、等等）。大家知道，Type I后果更严重，所以对扭曲变量的控制更有必要（也正因为如此，发现扭曲变量往往会令人兴奋甚至亢奋。）

表一、压抑变量与扭曲变量之一览表

	G as a Suppressor	G as a Distorter
Change in Significance-level
Nonsig->Sig	Y	-
Sig->Nonsig	-	Y
Change in Strength
Small->Large	Y
Large->Small	-	Y
Change in Direction
Postive->Negative	-	Y
Negative->Positive	-	Y

Source: J. J. H. Zhu (2009), All rights reserved.

回到你的数据，很显然，G是一个扭曲变量，所以一定要引入模型，原先的b_FE是错的而b’_FE是对的（当然，假定没有其它第三者的缺失）。至于G是否也是一个压抑变量，则要看b_FE和b’_FE的数值和各自的显著水平才能知道。你不妨补充报告一下，以飨读者。

也许你还会问，为什么G会改变原先关系的方向？我记得曾在以前的帖子中讲过（但一下子搜不到），G与E（即r_EG）或G与F（即b_FG）的两对关系中，必定（而其只能）有一对是负的（请你验证一下）。这是因为任何一组完整（即此外没有其它显著的第三者）的三角关系之乘积（即r_EG X b_FE X b_FG）必须为一个正值（见图2）。传播学中的cognitive dissonance理论就是据此而来的（以下12字为广告：详见我译的《大众传播模式论》）。

如果想更进一步探讨这种三角关系的话，那么可以将G当做是一个交互变量来处理（事实上G与E的交互项往往就是显著的），其结果大多有助于解开这种扭曲现象之谜。我记不得是否曾经说过，一般说来，交互影响比中介影响更有“革命性”意义。That’s why I was excited, rather than depressed, when reading your message.

如何选择Intraclass correlation coefficient (组内相关系数) 的模型？

Liu Yang @ 2009-05-15：

祝老师：您好！经常来您这看看，获益非浅。有一个问题想向您请教。我现在在做一个关于学龄儿童健康行为问卷的重测信度研究。如在过去一周你有几天参与体力活动至少60分钟？选项 1，2，3，4，5，6，7 天。因为数据是interval level，所以打算计算ICC。根据组内效应和项目效应是否随机，Single Measure ICC有三种类型，ICC(1,1), ICC(2,1) 和 ICC(3,1)。按我的理解，学生在不同时间回答同一道问题可以认为是two same judges in different time with fixed effect，因此应该采用ICC(3,1)。但是看过去的文献，针对同一道问题，如上题，三种算法都被用过，所以比较迷惑，希望您能指点，谢谢！

庄主 @ 2009-05-17:

你提到的ICC，指Intraclass Correlation Coefficient（通常翻成“组内相关系数”）。ICC在心理学和教育学研究中用得较多，但本庄大多数读者来自新闻传播学界，可能不甚了解，所以我先简单交代一下有关背景。

ICC涉及到多种用途，含义各有所不同。你是将其用于检验变量的信度（reliability），所以我这里也就仅谈谈信度检验中的ICC模型问题。（但是，要真正理解ICC，还是应该放在ANOVA的框架下进行。以下涉及到一点ANOVA、但我无意从ANOVA的ABC讲起，只假定大家已经掌握了。）

有人也许会问，检验信度不是已经有Cronbach’s alpha，为什么还要用ICC？这与被检验的变量之性质有关。我们通常检验的“信度”是指 the consistency between two or more concepts（两个或更多概念之间的一致性），这时我们确实是用Cronbach’s alpha，其实alpha只是根据Pearson r（即经典的相关系数）而计算出来的衍生物，而Pearson r 则是一种Interclass Correlation Coefficient（注意其中的“Interclass”，即“组间相关系数”，与ICC是相反的一对统计量）。相反，如果我们想检验的信度，涉及到的却是 the stability between two or more measures of the same concept（同一个概念的两个或多个测量指标之间的稳定性），这时Pearson r及其衍生物Cronbach’s alpha不不合适了（参见我的旧贴Difference vs. Correlation，虽然文中没有出现组间和组内相关的名词，但谈到的是同一问题），而可以用ICC。你面临的“健康行为”的“重测信度”，就是涉及一个概念（健康行为）的两个测量指标。内容分析中的inter-coder reliability也是一个概念（即内容分析的某个变量）的多个coders决策之间的稳定性。

顺便提一下，在ICC研究的文献中，上述“同一个概念的不同测量”是被叫做“different variables of a common class”。这里所涉及到的名词，如class,cases, variable（以及可能会出现的measurements, raters, judges, items, objects等等），如果翻成中文、都很容易产生望文生义的误导。不知你的迷惑，是否与这些名词有所关系？我一开始接触有关文献时，也曾迷惑过，后来把ICC的公式（右下）与Pearson r公式（左下）比较一下，就清楚了这些名词的真正含义。所以，我们还是不能不看公式。

在r的公式中，x_i和y_i分别是概念X和Y的测量值、和分别是X和Y的均值、S_x和S_y分别是X和Y的标准差，n是样本数。（由此可见，X和Y的取值范围可以完全不一样，如X可以是从-1到1而Y可以从0到10000；两者的标准差也由此可以完全不一样。其结果根本不会影响r的值。）而在icc中，为了强调“组内”的意义，我将X改写成X₁、Y改写成X₂（当然改写前后变量并没有本质区别）。两个公式的真正区别在于均值及标准差的计算，r中的X和Y均值及标准差是分别独立计算的、而icc中的是X₁和X₂的pooled mean（联合均值）、而也是X₁和X₂的pooled variance（联合方差、即联合标准差之平方）。由于ICC值是每个观察值减去“联合均值”（而不是各自的独立均值）、加总后再除以“联合方差”（而不是除以各自的独立标准差之乘积），所以其计算结果反映了“组内”的相关系数。（注意，“联合方差”背后有一个更严格的要求，即X₁和X₂的方差要相等。这一要求不是很容易满足的。如果你的两次测试之间有一定的时间间隔而其中有发生过什么重要的事件，如学校开设了卫生课或召开了运动会，使得学生之间健康行为的差异缩小了或扩大了，那么就不适合用ICC了。）

好了，在上述简单背景的基础上，我们来讨论你的问题：如何检验ICC？具体来说，就是如何选择合适的ICC模型。让我们从计算ICC所需要的数据结构说起（右图）。图a是最常见的结构，其中每个row（行）代表一个case（本例是ID从1到n的学生），每个column（列）是同一概念的某个观测指标（本例中是X₁和X₂前后两次观测），每个cell（格）中是每个学生的每次观测值（即上述公式中的x_1i或x_2i，在本例中取值1到7）。按ANOVA的术语，每个x_i受到三个来源的影响：一是between-columns effects（在本例中是over-time effects，但内容分析的inter-coder reliability则是两个coders之间的coder effects、等等）；二是within-columns effects（在本例中是within-subjects effects，即每个学生的特定因素）；三、无法被columns和rows所解释的残差。三者之间，残差和within-columns effects 总是（假定为）random（随机）的，前者是ANOVA能够成立的必要前提、而后者则是因为n个学生是从N总体中随机抽取的一个样本。剩下的between-columns effects则需要根据研究设计、数据采集方式等各种因素而来确定是fixed（固定）还是随机的，因此而形成了你所提到的三种模型：

Source of Variance	One-way Random Model ICC (1)	Two-way Random Model ICC (2)	Two-way Mixed Model ICC (3)
Within-columns effects	Random	Random	Random
Between-columns effects	--	Random	Fixed

首先来看ICC(1)。它并不考虑X₁和X₂的区别，所以实际上是将数据表中的X₁和X₂两列数据合成一列（即图b的结构，其中共有2n行），为了说明图a和图b的相等性，我在图b中加了变量Time，但实际上ICC(1)模型是估算Time的，而是只含一个因子（即自变量）的one-way ANOVA（单因子方差分析）。其自变量是ID，当只有两个重测指标时，自变量的values（即unique的ID数）很多、但每个value下面只有2个cases（所以是个很奇怪的模型），其F值是用来检验每个学生的均值全部为零的假设。由此可见，ICC(1) 并不能检验X的重测信度（当然它有很多其它用途，尤其是作为一个基准模型）。你说看到“过去的文献，针对同一道问题，如上题，三种算法都被用过”。我很难想象这种情况。建议你搞清作者用ICC(1)检验的零假设到底是什么。

回到图a的常见数据。如上所说，它可以用来同时分解columns和rows的影响，也就是ICC(2) 和 ICC(3) 所需要的数据。所以ICC(1) 和 ICC(2) 都可以用来检验重测信度。两者的区别在于如何看待我开始时说的“同一概念的各种测量指标”的产生机制。这不是一个统计问题、而是研究设计问题或数据采集方法问题，即取决于每个研究的具体情况。一般而言，如果X₁和X₂是该概念的所有可能测量指标（最极端的例子是“匹配”样本，如夫妻、双胞胎、师生、上下级等“对子”对同一问题的回答），那么它们应该是fixed。反之，如果该概念除了X_k和X₂之外，还可以有X₃、… X_k指标，那么它们应该是random的。同理，检验在内容分析的inter-coder reliability时，coders应该都是从一个理论上无限大的总体中抽出来的样本，所以也应该是random的。你说你的两次测试是“two same judges in different time with fixed effect”，我没有足够信息来否定你，但直觉上感到它们是无限空间中的两个时间样本点，所以为什么不是random的？

我们还可以从模型结果的使用来理解between-columns effects到底是fixed还是random的。如果你只想（或只能）将其结果限制在本研究的具体时空中（如这两个特定测量时间点、这两个特定coders、等等），那么可以采用fixed模型（3）；反之如果你希望将结果推及其它时间或空间（其它任何测量时点、任何coders、等等），那么就应该用random模型（2）。

除了between-columns effects的不同选择之外，ICC还涉及其它两个层面的选择，一是估算的ICC是consistency还是absolute agreement（两者的差别就是我上面提到的旧帖中描述的correlation与difference），二是single 还是average。这些分别涉及到一些新的问题，暂且不谈了。

如果谁真的要用ICC，应该认真读一下ICC的权威文献：K. O. McGraw & S. P. Wong (1996). Forming inferences about some intraclass correlation coefficients、以及该文的纠错补充。

最后，想说几句感受。常有网友在此问及各种进阶的统计问题、如SEM、multilevel、ICC等等。我是又喜又愁。喜的是后生可畏，敢于玩前沿。愁的是（从提问中推测），有关网友缺乏必要的基础知识，借助于统计软件而捷径上山、一步到顶峰。定量分析与其它绝大多数知识不同，只能循序渐进、一个台阶一个台阶往上爬。如果对进阶的方法不甚了了，与其大胆试用（大部分情况下会用错，而且错了还不知道原因何在），我强烈建议使用熟悉的经典方法，如回归、方差、crosstabs等等。经典方法也许用到你的数据上会有些问题、但那是已知的问题，而新方法可能带来的风险是无法预知。如果医生不了解某一新药，绝不敢乱用，而会使用已知作用有限并有副作用的旧药。我们是给数据看病的Data Doctor，也要有如此的基本医德。共勉。

不要做Modification Indices的奴隶！

Erin @ 2009-05-07:

有时在Lisrel的out文件中，有条message说“No Non-zero Modification Indices for PHI”，有时得到“No Non-zero Modification Indices for Lambda-x”或“No Non-zero Modification Indices for Lambda-y”。没有给出MI是因为什么？是因对相应的矩阵的设定么？

庄主 @ 2009-05-11:

理解这个问题的关键是弄懂Modification Indices (MI，修正指数) 到底是个什么东西，如它从何而来、说明什么、如何解读、等等？

简单说来，MI是将你现有模型的拟合度（Chi-squares）与如果你对某一没有被估计的参数（即fixed parameter，如PHI、Lambda等）作出估计（即改成free parameter）后模型的拟合度之间作比较的差别，其值也是一个Chi-squares值。(这句话也许用英文来表达更容易理解：A modification index tells the difference in the goodness-of-fit (as measured in Chi-squares) between an existing model and a modified model in which a fixed parameter (such as PHI or Lambda) is free to be estimate.）

左图是一个范例。假定你根据理论而设置了一个含X、Y和Z三个隐含因子的测量模型，其中X是观测变量X1-X3的来源、Y是观察变量Y1-Y3的来源、Z是观测变量Z1-Z3的来源，而三个因子之间容许存在一定的相关程度（注意X、Y和Z之间的双向箭头）。你在LISREL或AMOS里，用该模型对某数据做了拟合，发现其拟合度为显著（即模型与数据有显著差别）。为了改进模型的拟合度，你查看了LISREL或AMOS给出的MI结果，看到上述的“No Non-zero Modification Indices for PHI”，但是在 Modification Indices for LAMBDA-X（以下简称LMI）和Modification Indices for THETA-DELTA（以下简称TDMI）中，各有一组数值。比如，LMI中最大的是Lambda_y1X = 10.555、TDMI中最大的是Delt_z2z3 = 12.222，其次是Theta_x3z1 = 8.333。它们分别说明，如果你将Y1加到因子X上去，修正后的模型的Chi-squares会减去10.555；或者如果你在Z2和Z3的残差项之间建立相关关系，新模型的Chi-squares会减去12.222；或者如果你容许X3和Z1的残差项之间相关，新模型的Chi-squares会减去8.333。（注意：如果你同时做两项或三项修正，新模型的Chi-squares不一定会减少10.555+12.222+8.333之和那么多。）我们知道，在一个自由度的条件下，Chi-squares的显著性临界值为3.84，也就是说，如果一个MI的值大于4，就值得注意了。

那么，为什么LISREL或AMOS有时会“罢工”，不报告MI呢？简单说来有两种情况：一是你的“所有可估计参数”(all estimable parameter）已被全部用完。注意，这里的“所有可估计参数”不等于“所有参数”。如上例的理论模型共有45个自由度（如果你不能一眼看出来，说明还得看点书再来玩SEM），其中估计了21个参数（如果你连这个也看不出来，那就麻烦了），还有24个自由度，也就是说还可以估计24个参数。但是，在PHI矩阵（外生因子的方差-协方差，详见“LISREL的八个矩阵”）中已经没有可用的参数了，因为X、Y、Z三者之间的三对相关关系已经用尽了其所有的信息。所以，如上所述，LISREL或AMOS已经发了No Non-zero Modification Indices for PHI的“罢工通知”。事实上，除了PHI之外，结构模型的其它参数（other parameters of structural model），如GAMMA（外生因子对内生因子的影响）、BETA（内生因子对内生因子的影响）、PSI（内生因子的方差-协方差）等，也经常没有MI，因为它们多半已按理论模型的假定而被用尽。说到底，结构模型参数是绝大多数研究的最终目的，谁会将它们闲置在一边，等到看过MI之后再做决定是否进行估价？（我还会回到这一点的。）

但是，测量模型的参数（parameters of measurement model）还有大量闲置的参数。如本例中的LAMBDA矩阵中，还有18个可被估计的参数（包括X对Y1-Y3、X对Z1-Z3、Y对X1-X3、Y对Z1-Z3、Z对X1-X3、Z对Y1-Y3），THETA-DELTA中则有更多（36个）参数可以被估计。 当然，你不可能将它们（总共54个）穷尽，因为你只有24个自由度。你甚至不应该将自由度全部用掉（见后面的讨论）。这里先回答一下，为什么LISREL或AMOS有时不提供其中某些参数的MI？这是没有MI的两种可能之二，即你的原始模型虽然拟合得不太好、但相比任何一种其它的修正模型来说，它的拟合度是最好的，这往往是观测变量之间缺乏任何关系造成的。当然，这种情况较罕见，尤其是你的模型有两个或以上隐含因子时，总会有某个没被估计的测量模型参数可以修正的吧？总之，一切从自由度出发，做任何事前先看看你还有多少自由度？这些自由度存放在哪个矩阵里？

总之，如果LISREL或AMOS没有提供某一参数或某一矩阵（某类参数的的集合）的MI，说明该个或该组参数或者无法估计（结构性的问题）或被估计之后并不能给现有模型带来任何改进（实证性的问题）。由此看来，MI是个不错的工具，它可以帮助我们找到改进模型拟合度的“捷径”。但是，盲目使用MI，也会造成很多错觉或谬误。在我看来，不知情者对MI的误用和知情者对MI的滥用，是SEM应用中的一个主用问题。何谓“误用”、何谓“滥用”？我无意写篇论文来讨论，仅以上图中的三条虚线为例，说一下我的看法。

1、一般情况下，不要碰LAMBDA，即不要仅仅根据MI而增添cross-factor loading（跨因子负荷？），如上图中根据Lambda_y1X 的值而将Y1挂到X上去。估计跨因子负荷是EFA的做法，也是EFA为人诟病的一大原因。Y和X可以相关（如图中已做到了）。但是，如果再将Y1连到X上去，确实可以改进模型的拟合度，但同时牺牲了Y（以及X）因子的效度，得不偿失。也许有人说，我的理论要求Y1同时受X和Y的影响，怎么办？记住：everything is related to everything的理论一般不是好理论。

2、在任何情况下，绝对不要碰DELTA（或EPS），即不要在一个因子内部的各变量之间增添correlated errors within a factor ，如上图中的Delt_z2z3 ，不管其值有多少，也不能将其释放出来估计。一个因子中的各变量之间的相关部分，已经充分反映在它们在该因子的负荷之上，如果再将各变量的残差连起来，说明该因子之内还有因子，这在理论上是说不通的。当然，如果一个因子下各变量之间出现很大的MI值，说明这个因子模型有问题，也是该因子不是unidimensional的、也许是某变量有异常值（或者严重偏离正态分布）、等等。这些问题，需要通过清理数据或调整模型、而不是简单的在因子内变量残差建立相关关系。

3、在一定条件下，可以考虑估计THETA中correlated errors between corresponding observed variables cross factors（跨因子对应变量残差之间的相关系数），如在上图中的Theta_x3z1 。这里的“一定条件下”的“对应变量”，往往指不同因子之间的两（或多）个变量之间是采用相同的测量方法（如问卷中相同的提问及回答）、或者同一变量在不同时间点上的测量值、等等。这时，建立其残差的相关关系，就相当于在各因子之间建立一个测量方法之共同因子（或者为MMMT模型的做法）。

总之，正确使用MI的关键，取决于我们的目的是什么？是为了提高模型的拟合度以便能够发表、还是为了改进模型的结构参数以降低Type II误差？如果仅是为了前者，即使能够蒙过审稿人、也无法混过所有读者的仔细阅读。而如果为了后者，那么我开始时的叙述其实已经暗示了，MI对结构参数往往没有什么帮助。

如何检验一个同时为调节和中介的变量？

Anonymous @ 2009-04-22：

祝老师您好： 我想请问两个困扰很久的问题：1.是否可能存在着这样的情形：在变量a对变量b有影响的前提下，变量c对它们之间关系的中介效应和调节效应同时存在？2.在用SEM做全显变量路径分析时，应该怎样看待这些拟合指数，是否和做CFA或结构模型的标准完全一样？

庄主 @ 2009-05-01:

我还没有见到过这种理论或这类数据。我估计，如果有某理论能合理假设出这种情形（你能否举个例子？），test（检验）并不难（见以下讨论），但却很难verify（证明），因为交互关系和中介关系各自都是不容易验证的小概率事件、而两个小概率事件交将是一个特小概率事件（传说中的“黑天鹅”事件？）。

说说如何检验交互关系+中介关系吧。当然需要借助公式和图像来说明。为了与为我其它帖子使用的符号一致，我将你的a、b、c分别改为X（自变量）、Y（因变量）和Z（调节和中介变量），并生成XZ（交互变量）。以下分别是交互关系、中介关系和交互+中介关系的模型：

注意：为了简便起见，三个模型都省却了常数项。模型a和模型c中的X、Z、XZ之间都假定为0相关。模型2和模型3中的b1也都假定为0。

模型1和模型2是用来说明模型3的来历，而模型3是需要被检验的模型，具体步骤为：

1、中介关系的检验：估计模型3（包括b1）、然后设b1为0，比较两者的拟合度，如果没有显著差别，则说明b1=0；如果b2和b4同时显著地不等于0，并且b2b4显著地大于b1，则中介关系成立（具体参见如何检验两个中介变量的效应?和其它帖子）；

2、交互关系的检验：估计模型3（包括b1)、然后设b3为0，比较两者的拟合度，如果没有显著差别，则说明b3=0、反之，如果有显著差别，则说明b3不等于0、即Z对X与Y的关系有交互作用（具体参见以前发过的好些交互影响帖子）。

如果X、Y、Z都是直接观测变量，那么上述模型只是不含测量模型的路径分析，可以在SEM来做、也可以用经典的OLS回归来做（即分别执行图c标题中的两个公式就是了），其结果完全一样。SEM的拟合度可以用卡方值或R平方、而回顾的拟合度则用R平方。但是，这时的SEM的卡方值与CFA的卡方值之含义完全不同，前者是结构模型中因子之间的关系而后者是测量模型中因子与观测变量之间的关系。

如果X、Y、Z中有带观测变量的隐含因子，问题就复杂了很多，因为现有的SEM模型对交互项（XZ）没有完善的处理方法，一般是采用分组方法，即将样本按Z的不同值分成若干组，分别估计图b，然后通过比较各组b3的差别来验证Z的交换作用。

如何确定综合指数的构成权重？

Anonymous ＠ 2009-04-29：

祝老师，您好！我现在在写硕士毕业论文，想请教您几个小问题。
我让主管给下属的三种绩效（任务绩效、情境绩效和反生产绩效）做出评分，然后对员工的总体绩效（与前面相独立的量表）做出评分，然后用三种绩效的得分对总体绩效得分进行回归，这样得出三个回归系数。前两个系数显著，后一个不显著。这三种绩效的系数可以视为主管在评价员工总体绩效时更看重哪种绩效，即一种权重。我想考查哪种绩效在总体绩效评分中更受主管重视，我还需要进行两个系数的显著性差异的检验吗？如果要，如何做？

Anonymous @ 2009-04-29（也许是另一读者）：

他的意思应该是这样说,已经有若干个观测变量，这些变量为了测量隐含变量(总体满意度)。但由于理论上不同的观测变量对总体变量的影响程度是不一样的，对隐含变量的贡献程度不一样，系数也就不一样，不能通过全体简单的平均得出结果。那么,得通过什么方法来确定每个观测量的权重，再配合每个观测变量的均值来求得最终的隐含变量呢？结构方程中的路径系数是否可以作为这个权重来理解呢？

我也想顺便问一下，相关系数R平方是否也可以作为权重？回归系数呢？有的文章是通过因子分析，用共同度来作为对总体的权重系数，这个处理方法合理吗？

庄主 @ 2009-05-02：

上述两个问题应该是不同的。匿名一（大家提问时能否留个名？当然假名虚名浪名都可以，以便区分）的问题是一组supervised数据，即总体绩效是一个观测到的变量，而匿名二的问题中因为总体绩效是没有观测的隐含因子、所以是一组unsupervised数据。两者之间当然后者更常见，但前者含有更多信息、因此可以研究更多问题。

一、先讨论匿名一的问题。他（她？）的模型应该是（见最后的注释）

Y = b0 + b1y1 + b2y2 + b3y3 + e                        （公式一）

用来检验y1 - y3各自对Y的影响（即其所说的“考查哪种绩效在总体绩效评分中更受主管重视”）。是否需要对b1与b2、b1与b3、b2-b3三对系数之间的差别做显著检验？当然要。如何做？请参见前贴“如何检验两个回归系数的差别？”。

二、匿名二提出的是一个含三个观测变量的测量模型（measurement model），即

y = Λ_yη + ε                                                       （公式二）

其中y = y1，y2，y3，η是隐含因子、Λ_y 是η对各y的影响（也即权重），ε是各y中不受η影响的独自变异（也即误差）。显然，公式一与公式二很不一样：总体绩效在公式一中是因变量（等号的左边）而在公式二中是自变量（等号的右边）；公式一中的b1 - b3无论在理论上还是在数值上都与公式二中的Λ₁ - Λ₃是不同的。

三、现在分别讨论匿名二提到的四种确定y之权重的方法：

1、结构方程中的路径系数：英文为path coefficients of the structural model，但本案没有path coefficients、只有factor loadings of the measurement model（测量模型的因子负荷，即公式二的Λ₁ - Λ₃）。答案是肯定的，因子负荷就是被当做y1 - y3的权重的。

2、相关系数R平方：不清楚你指的是y1 - y3之间的两两相关系数之平方，还是公式二的R平方？前者与匿名一的研究问题无直接关系。后者就是Λ₁ - Λ₃的平方。

3、回归系数：同样不清楚你指哪个“回归模型”？如是公式一，你没有直接观测的Y，无法估计。如是公式二，就与你的方法1相同。

4、因子分析的共同度(commonality)：这里指的应该是exploratory factor analysis，既然现在有理论导向的confirmatory factor analysis（即公式二），就不必再用数据导向的EFA了。

四、有心的读者也许会想到将匿名一的supervsied数据和匿名二的unsupervised数据（两者中的y1 - y3是相同的）合在一起考虑，就是说，先用公式二构建隐含因子η，然后再检验其与观测变量Y之间的相关关系。一般说来，η与Y是正相关的，但其相关程度不一定是很强烈的、甚至不一定是显著的（如果样本小的话）。其背后有两种可能性：一是方法上的问题：虽然η没有测量误差、但Y含有一定的测量误差（但无法估计），二是理论上的问题：η与Y不一定是一个概念（如η也许是一个多维的因子，其中某些维度与Y无关），即confirmatory validaity问题。如果数据中只有Y和y1 - y3四个变量，我们无法将这两种原因分开。如果有其它“第三者”变量（在理论上与Y或测量误差有关），则可以进一步解析下去（重大突破往往就在眼前了）。但是，即使只有这四个变量，据此而发现的η与Y的相关关系，已经提供了很多信息（如对η效度的独立验证）。

最后，讲一讲语言的精确性问题（应该是已讲过多次的老话了）。匿名一说“用三种绩效的得分对总体绩效得分进行回归”，这句话大概是说倒了的，而本意应该是“用总体绩效得分对三种绩效的得分进行回归”（即公式一）。而匿名二的本意才是“用三种绩效的得分对虚拟的总体绩效得分进行回归”（公式二），但他（她）提到的方法3又和公式一混起来了。思想的迷惑往往与语言的含混互为因果。如何避免？用公式和英文。在英文里描述回归模型的句型是

regress Y on X controlling for Z，或者Y is regressed on X with Z controlled

其中Y、X和Z分别指因变量、自变量和控制变量。这使我联想起前几天与一些学生聊天的情景，当时我建议他们学研究方法时不要看中文书，因为中文语言不够严密，不料遭到强烈质疑，要我举例证明。这里是又一例。如果依靠他们的中文描述，很难将匿名一和匿名二之区别弄清楚的。

如何检验两个中介变量的效应?

flyingzjt @ 2009-04-21：

经常看贴，收益良好，今天请教一个问题：X影响Y的关系中有两个中介变量A，B，如果A与B相关，那么其中介效应如何确定，其大小可以比较吗？如果有两个自变量X，Z，中介变量仍为A，B，可能的影响为X－A－Y，同时Z－B－Y，且A与B相关，X与Z相关，那么两个中介变量的效应又如何确定，如果上述变量均为潜变量，如何用LISREL与AMOS检验中介效应？多谢多谢！

庄主 @ 2009-04-25:

你的问题叙述出来好像挺复杂，但如果先画个图（见下图b）再来看，就属常见并较简单的模型之一了。（注意，为了与我在“八大矩阵”中用的符号一致，我用γ表示从X和Z出来的影响而用β表示从A和B出来的影响；其它的系数如φ、ψ、ξ等也来自“八大矩阵”。）

 

 

 

 

 

 

我估计你已经知道，中介效应需要满足以下条件：

1. 在中介变量（A或B）没有起作用之前（如图a），自变量（X或Z）对因变量（Y）有显著的direct effects（直接影响，即β_YX或β_YZ ≠ 0）；
2. 当A或B出现之后（图b），X或Z通过A或B而对Y有显著的indirect effects（间接影响，即γ_AX或γ_BZ ≠ 0以及β_YA或β_YB ≠ 0）；
3. X或Z对Y的间接影响大于其直接影响（即γ_AX × β_YA > γ_YX 或γ_BZ × β_YB > γ_YZ ）；
4. 当A或B起作用之后，X或Z对Y的直接影响随之彻底消失（即γ_YX或γ_YZ = 0，这就是为什么我在图b中用虚线表示相关的线条），

注：如果只满足条件1-3，则可认为存在weak version （弱版本）的中介效应；而如果条件1-4均被满足，得到的则是strong version（强版本）的中介效应。

根据上述条件，我们可以很容易地在SEM中检验中介效应。在本例中，由于涉及两个中介变量，可以分以下几步做：

1. 检验“直接影响”模型（图a），如果其中的γ_YX 或γ_YZ 为显著，则条件1成立；
2. 加入A和B而构成一个full model（“全模型”，图b），如果其中的γ_AX 和β_YA同时显著、或γ_BZ 和β_YB同时显著，则说明条件2成立；
3. 如果全模型中的γ_AX × β_YA > γ_YX 或γ_BZ × β_YB > γ_YZ （前者即LISREL、AMOS等软件中报告的X或Z的间接影响值、而后者则是报告的X或Z的直接影响值），如果两者有显著差别，则说明条件3成立；
4. 如果全模型中的γ_YX 或 γ_YZ 不显著，则说明条件4成立。

如何检验时间序列数据中的自相关？

happyle @ 2009-02-22:

关于一元线性回归的问题
用一次考试的成绩预测另一次考试成绩，建立回归方程。。。显著性检验。。。
F检验、T检验都有统计学意义
回归标准化残差直方图正态分布
P-P图正态分布
因变量与回归标准化预测值散点图呈直线趋势。。。
但是。。。
D.W.=.815
这表明残差之间正相关，不是相互独立的
所以请问下，这时候考虑DW值是否有意义？

庄主 @ 2009-04-18:

首先要抱歉没有及时回复你的问题。我写帖子的时间不多，每次从收到的问题中按我对读者的兴趣判断挑一个。你的问题有一定的技术含量、但比不上近期的其它题目更有普遍兴趣。

其次提个建议：以后能否将你的问题用sentences（句子）而不是bullet points（词汇排列）表达出来？不知是否受到PPT讲义的影响，越来越多的学生提问时采用这种方法。虽然简要，但如果简略到意义残缺，就适得其反了。准确地描述问题，是学好定量分析的基本功之一。

好了，回到你的问题。先为其他读者介绍一下背景：DW（Durbin-Watson）值是检验一组时间序列数据中自相关(autocorrelation) 程度的统计量。更准确地说，DW检验的是零假设为：一个为时间序列的因变量Y_t在对若干（1至k个）自变量作回归之后的每个时间点的residual（残差，记为e_t）与其前一时间点的残差（e_t-1）之间的相关（记为 Cor(e_t, e_t-1)）= 0。这种自相关，也被称为 first-order autocorrelation，简称AR1，中译“一阶自相关”，这里的所谓“一阶”是指两个残差之间相差一个时间点。

这里涉及好几个概念和问题：什么是残差（比较容易理解），什么是自相关（有点难度），一阶与高价自相关有什么差别（也有点难），自相关不等于0会有什么问题？等等。我只谈最后一个问题，因为与你问题直接有关，而其它留待以后有机会再谈。

简单说来，如果 Cor(e_t, e_t-1) = 0, 那就违反了OLS回归的基本要求之一（即残差之间的独立性）。如果残差之间有自相关，虽然不会影响回归系数的值，但会影响（低估）回归系数的标准误差（即自变量对因变量的显著程度，从而犯了Type I错误）。这是少数不可饶恕的“死罪”之一，而DW值就是判断是否犯了此罪的判决书。

DW值与Pearson r或其它相关系数不同，其取值在0至4之间，其中当DW值=2时，说明自相关=0；如果DW（明显）小于2，反映有正的自相关(positive AR)；如果DW（明显）大于2，反映有负的自相关(negative AR)。两者相比，前者（正相关）更为常见。这里又出现一些新的概念和问题，如什么是正的自相关、什么是负的自相关、怎样才算明显小于或大于2，等等。这里只谈最后一个问题，即DW对2的偏离到达什么程度，就是“明显”或“显著”差别了。

与其它许多统计检验的做法（一般是将统计值除以其标准误差）不同，DW的统计检验比较复杂和繁琐。Durbin与Watson编制了一套检验表，分别对应于不同的数据时间点、不同的自变量个数和不同的显著水平（分为0.01和0.05两种），提供两个临界值，分别记为D_L（下限，低于其者则绝对有自相关）和D_U（上限，低于其者“也许”有自相关）。具体使用如下：

1. 观察到的DW值小于2（即正自相关）时：
   1. 如果DW大于D_U，说明总体中的Cor(e_t, e_t-1) = 0，即可以接受回归分析结果；
   2. 如果 DW小于D_L，说明总体中的Cor(e_t, e_t-1) ≠ 0，即不能接受回归分析结果（因为自变量与残差之独立性被破坏而使得回归结果不可靠）；
   3. 如果DW落在D_L和D_U之间，则是一个灰色地带，需要进一步根据你的自变量分布是否均匀（即X在自己的各个取值上是否平均分配）来决定。如是，则按1b办；如否，则按1a办。
2. 观察到的DW值大于2（即负自相关）时：
   1. 如果DW小于4-D_U，则如同1a，即总体中的Cor(e_t, e_t-1) = 0而可以接受回归分析结果；
   2. 如果DW大于4-D_L，则如同1b，即总体中的Cor(e_t, e_t-1) ≠ 0而需要拒绝回归分析结果；
   3. 如果DW落在4-D_L和4-D_U之间，则如同1c，是一个灰色地带，需要进一步根据你的自变量分布是否均匀而决定是参照2a还是2b。

上图是我从DW表中选出的三组临界值，其显著水平均为p = 0.05，时间点在10至100个之间，自变量个数分别为2、4和6个。从图中可以看出如下规律：一、当时间点小于20而自变量为4个以上，D_U接近甚至大于2（即数据一定有自相关），而且D_L与D_U之间存在巨大的灰色地带；二、随着时间点增加至30以上，D_U变得相当稳定，而D_L与D_U之间的灰色地带逐渐缩小；三、D_L与D_U之间的差距并不是对称的。这些都有助于我们理解时间序列分析的基本要求（如数据时间点至少要30个以上、自变量个数不能多）的来源，同时也说明一些“常规说法”（如DW值不能小于1.0）其实并不准确。

你做的是一元回归方程，说明有1个自变量，得到的DW值为0.815，显示存在正的自相关。你没有交代数据的时间点，但可以从上图的红线中看出，你的DW值一定是低于临界点下限的。

你问：这时候考虑DW值是否有意义？当然有意义：你数据中有显著的自相关。我猜你的原意是“这时候回归分析结果（如回归系数达到显著水平）是否还可靠？”前面提到，在显著的自相关下，回归系数的标准误差被人为缩小而显著水平被人为提高，所以也是不可靠的。

当然，你的数据也许不是时间序列 (Y_t = b₀ + b₁X_t) 而是panel数据 (Y_it = b₀ + b₁X_it) ，因为你说用“考试成绩2预测考试成绩1”，暗示该数据中只有两个时间点，但应该有i个人。如果是这种i x t的数据（注意panel公式中的下标），不能用上述经典的DW检验，而应改用修正过的DW公式。SAS、Stata等软件中有，但SPSS13版（我不知14版以后的情况）并不提供这一统计量。