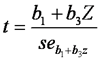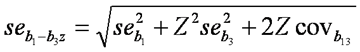yxf @ 2009-12-29:
庄主您好:我是一名博士生,怀着非常忐忑的心情给您写这篇文章。我经常拜读您竹家庄上的文章,受益很深。您在2009年4月11日文章“如何绘制调节效应的图形?”,我能够看懂,但是用您的绘制调节变量的图形的方法于下面这篇文章得出的回归系数,和该文章得出的回归系数,为何不同?
这是发表于《管理世界》2009年第一期的一篇文章(下面复制了它的两个图和一段文字)。
首先,根据您的绘制调节变量图形的方法,
Y = 0.405X + 0.360Z - 0.186XZ + 常数 =(0.405 - 0.186Z)x + 0.360Z+常数
(1)低中国人传统性,取Z为均值减一个标准差,为-0.647,此时Y = [0.405 - 0.186 × (-0.647)]X + 0.360 × (-0.647) + 常数 = 0.525X+常数
(2)高中国人传统性,取Z为均值加一个标准差,为0.647,此时Y = [0.405 - 0.186 × (+0.647)]X + 0.360 × (+0.647) + 常数 = 0.525X + 常数 = -0.285X + 常数
但是,为什么这篇文章得出的结果不同呢?
(1)低中国人传统性,Y = 0.503X + 常数 (p<0.01)
(2)高中国人传统性,Y = 0.018X + 常数 (p>0.01)
这篇文章的结果正确吗,它是如何计算出来的,特别是它的p值是如何计算出来的?是不是我没有正确领会您的“如何绘制调节效应的图形?”的内涵?
(庄主注:yxf的信中附有原文的部分页面,因涉及版权,这里删去。有兴趣者请参阅:汪林、储小平、倪婧:“领导—部属交换、内部人身份认知与组织公民行为”,《管理世界》2009年第1期,97-108页。)
庄主 @ 2009-12-30:
你提了两个问题。一是如何计算“低传统”组和“高传统”组各自的回归斜率;二是如何检验这些斜率的统计显著水平?以下分别简答之。
一、如何计算分组回归斜率(也叫“简单斜率”)?我在多个前贴(包括你提到的“如何绘制调节效应的图形”一文)中已介绍过,简单斜率是根据总样本回归模型
Y = b0 + b1X + b2Z + b3XZ (1)
而计算出来的。即先选定若干个Z的值(如本例中小于和大于“传统性”均值的一个标准差,分别记为Z1和Z2),然后代入公式1,就有
Y = b0 + b1X + b2Z1 + b3XZ1 = (b0 + b2Z1) + (b1 + b3Z1)X (2)
和
Y = b0 + b1X + b2Z2 + b3XZ2 = (b0 + b2Z2) + (b1 + b3Z2)X (3)
其中b1+b3Z1是低传统组的简单斜率、b1+b3Z2是高传统组的简单斜率。这种方法,与论文作者所参照的Aiken and West (1991)的方法是完全一样的。
至于具体计算,只是做简单的加减乘,没有特别深奥的地方。当然,先要弄清Z1和Z2是原始数据还是取中值 (centered score)。在本例中,前者为3.52±0.647而后者为±0.647(因为取中值的均值为0)。你是用后者来计算的,你的结果中低组的斜率是对的(0.525),但高组的斜率错了,应该也是正数(0.285)而不是负数(-0.285)。我估计你算对但写错了。
作者为什么算出来分别是0.503和0.018?我看了原文,他们没有交代用的是原始数据还是取中值。如果用的是原始数据,结果应该分别是-0.129和-0.370,与其上下文不合。估计他们用的是取中值,但手算时出错了。你不妨直接写信问他们一下?
二、如果检验简单斜率的显著性?我在有关前贴中也应该讲过,但一下子查不出来,所以再讲一下。我们知道,一个回归方程的斜率(如b1),可以用t = b1/seb1 来检验。同样,简单斜率b1+b3Z的显著性也是用一个类似的 t-检验来完成的(注意,要将这里的b1+b3Z当做一个常数来看),即
其中的分母就是简单斜率的标准误差,SPSS或其它统计软件不会直接报告这个参数,但可以根据以下公式
手工算出,其中的se2b1和se2b3分别是b1和b3的方差(variance)、covb13是b1和b3的协方差(covariance)(注意:这里提到的是b1和b3的方程-协方差而不是X和Z的方差-协方差),在SPSS中在Statistics的选项中选择“BCC”可以获得这些参数,而这里的Z则用上述的Z1或Z2值来代入。
算出公式4的t-值后,就可以查表得出其相对应的p-值了。估计原文作者就是这么做的。当然,他们如果报告一下两个t-值和对应的两个p-值各为多少,就更令人信服了。
yxf @ 2010-01-07
庄主,您好:非常感谢您的回复。我非常仔细地学习了您的“如何检验交互效应的显著性?”,感觉帮助非常大。在您的回复中,“二、如果检验简单斜率的显著性?”有一段话
“简单斜率b1+b3Z的显著性也是用一个类似的 t-检验来完成的(注意,要将这里的b1+b3Z当做一个常数来看),即公式4(省略),其中的分母就是简单斜率的标准误差,SPSS或其它统计软件不会直接报告这个参数,但可以根据以下公式5(省略)手工算出,其中的se2b1和se2b3分别是b1和b3的方差(variance)、covb13是b1和b3的协方差(covariance)(注意:这里提到的是b1和b3的方程-协方差而不是X和Z的方差-协方差),在SPSS中在Statistics的选项中选择“BCC”可以获得这些参数,而这里的Z则用上述的Z1或Z2值来代入。”
这里,se2b1、se2b3、covb13在SPSS中的计算方法我不太确定如何操作,因为不知道BCC是如何操作的?我找到两种方法,您认为哪一种方法算出的协方差是适合本文这里使用的,因为这两种方法算出的协方差不一致:
- Analyze—>Regression—>Linear—>Statistics—>Regression Coefficients中 "Covariance Matrix” 打钩,然后算出协方差矩阵;
- Analyze—>Correlate—>Biraviate—>Options中 "Cross-Product Deviations and Covariances” 打钩,然后算出协方差矩阵。
您认为哪一种方法是正确的,还是都不正确?正确的方法应该如何操作?
另外,“covb13是b1和b3的方差-协方差而不是X和Z的方程-协方差”,这两个协方差有何区别?
万分感谢!
庄主 @ 2010-01-16:
用方法1而不是方法2。如我原文中所说,前者是回归系数(b1, b2, b3)之间的方差-协方差、而后者是自变量(X, Z)之间的方差-协方差,是风马牛不相及的完全两回事。
大家应该对后者很熟悉,即使不那么熟悉、但在学习初级统计的相关系数部分时、多半也看到过相关系数与协方差之间的转换关系(Covxz = rxzsdxsdz,即X和Z的相关关系rxz乘上X和Z各自的标准差sdx和sdz就是X和Z的协方差Covxz)。很多学生对我说,他们的老师没有讲过这个公式。我的回答一般是“这还需要讲吗?”。比较一下相关系数的公式和协方差的公式,前者不就是少了sdx和sdz吗?甚至记不得公式,但一定知道相关系数是标准化的协方差、而协方差是非标准化的相关系数吧?将一个标准化的指标乘上其标准差不就是其非标准化的指标了吗?反之,将一个非标准化指标除以去标准差不就是标准化了吗?当然,如果只是通过老师的PPT讲义和点击SPSS菜单而学习统计的话(很可惜,现在的社会科学学生中大概99%是这么过来的),这些ABC原理都好像很陌生。青年朋友们:不要做PPT和SPSS的奴隶,多看书、并且经常手工演算各种公式吧。
那么前者呢?很可能你们老师们没有讲过。其实我的老师们(当中不乏顶尖学者)也都没有讲到,因为回归系数的协方差一般用不到。曾有一位美国名校名导师培养出来的博士朋友问我,b1和b3是两个常数、它们之间怎么可能有相关系数呢?是的,回归系数是常数,但任何统计量(常数)都有一个抽样分布(即假定从同一总体中抽取无数个相同大小的样本,做同一回归而得到的无数个回归系数就构成了一个服从t的抽样分布),在这个抽样分布中的每个回归系数都是一个变量(而不是常数),所以各自都有自己的方差、而相互之间就有相关系数或协方差。