丫丫@ 2009-01-12:
一个非常困惑的问题向您请教:我在用amos检验模型A―B1/B2―C―D,其中B和C都是中介变量。B1和B2是B的相关但不同的两种形式,我想将B1/B2同时放入模型,看A对它们不同的影响,以及它们分别对C的不同影响。现在的问题是:
- B1和B2相关较高,在spss里面两者的相关系数是.683,做B1/B2到C的回归时Tolerance是.534,VIF是1.8,在amos用双箭头连接后显示两者相关系数是.90左右。我看到您前面的文章说“保守的学者认为相关系数不能超过0.7;自由派的则认为可以放宽到0.9”,而且Tolerance和VIF似乎也在可以接收的范围内。但是,在AMOS里如果我同时将B1/B2放入模型(此时B1/B2不能再用双箭头连接了),有一些标准化后的相关系数会大于1,结果很奇怪。但如果我将B1B2合并成一个变量B(其中B1B2各有两个dimension,合并在一起就是4个dimension成为一个B的construct考察),结果就又正常了。请问结果不正常的原因是我把B1B2分开了吗,这是否意味这B1B2不能同时放入一个模型了?如果希望同时放进去但不合并,该如何处理?
- 单独检验模型的后半部分B1/B2―C―D,此时B1和B2就可以用双箭头连起来,AMOS结果处理一切正常,但是两者的相关是.90,不知道这样报结果行不?
非常感谢。
庄主 @ 2009-01-16:
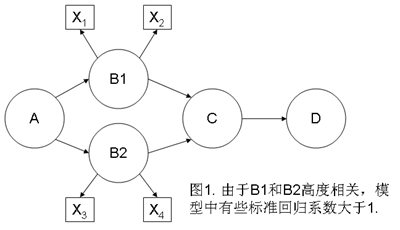
为了便于讨论、以及帮助其他读者理解你的问题,我画了以下几个图。图1是你希望检验但“结果很奇怪”(如因子之间的标准回归系数大于1)的模型。
针对上述问题,你在图2中将B1和B2合并成一个因子B,就解决了问题,结果也正常了(即回归系数等于或小于1),
但是,你并不满意图2,因为在理论上B1和B2是B的两种不同“形式”,所以你尝试将图1中的A去掉,结果也很正常。
图2说明,问题出在B1和B2的高度相关(0.90)上;但是,图3好像又暗示问题在于A而非B1-B2(因为拿到A之后问题就没有了)。所以感到“非常困惑”。不知上述图以及相关描述是否有误解的地方?
首先,我想到的是你的样本大小(你没有交代)。如果样本足够大,B1和B2的相关程度也许会减弱。
第二,你讲到,图1中的B1和B2之间不能建立相关关系(这是因为两者是endogenous variables 内生变量)、而在图3中两者之间又可以建立相关关系了(这时,它们成为exogenous variables外生变量)。但你没有提及,在图1的模型中,你是否估计了B1和B2的error variance(误差)之间的相关关系(即PSI矩阵,详见“LISREL的八个矩阵”一文)?如无,也许这是导致模型参数出古怪的原因之一。
第三,但是,哪怕你通过建立内生变量(B1和B2)误差之间的相关关系而使得模型参数正常,B1和B2之间缺乏discriminant validaty(差别效度)的问题仍然存在。你说,B1和B2是B的“不同的两种形式”。然而,数据告诉我们,这两种形式之间没有本质差别。根据parsimony(简约)原则,它们应该合二为一(即图2)。图2比图1少了两个参数(A->B2和B2->C),也即多了两个自由度,因此更可取。
图3虽然也能产生“正常”结果,但牺牲了A,虽然我不知道A的理论含义,但你的研究目的之一是检验A对B1和B2的影响,所以牺牲A是不可取的。
所以,三个模型中,只有图2是合理的。
最后,当然,你还可以试一下,在图1的B1和B2之上,建立一个second-order factor (二阶因子,见图4,参见二价因子分析的可行性vs.可取性等文)。由于B1和B2高度相关,这个含二阶因子的模型应该能够与图2的结果相似。
然而,图4比图2多了两个参数、也即少了两个自由度,所以不够简约。而且,A不能直接影响B1或B2、而要通过B来影响B1和B2;B1和B2也不能直接影响C,所以该模型也不能直接回答你的研究问题。
你的问题有相当的普遍性,即两个(或数个)概念在理论上是有区别的、但在实证中却没有discriminant validity。除非你换数据,否则,在现有数据的基础上,你只能接受现实,即将缺乏discriminant validity的概念合并起来。