如何判断统计显著的差别是否具有实际意义？

丁丁 @ 2009-10-02：

老师，您好！我想问一个关于样本量的基础问题。通常我们有公式可以计算理论最小样本量。但我想问有没有最大样本量，不得因为如果样本量足够大，我可以证明任何没有实际意义的差别是不是statistically significant。比如说，3.75和3.50，SD 都为1.00，如果样本量个为100，不显著。如果是200，就显著了。同理，3.50和3.55，如各有10000，也显著了。但是没有实际意义。我看到很多研究就用这种方法，研究出了很多correlation significant的结果，或两者显著不同的结论。我觉得不对，却没有理论去说它不对。难道真如某人所说, 统计学家可以证明任何事吗?

庄主 @ 2009-10-31:

抱歉，拖了将近一个月才回复你的问题。最近较忙，忙的原因之一是做有关博客写作的可持续性研究（好像就是在研究我自己为什么不能持续写博客）。

你的问题涉及了样本量和统计显著性两个概念，为了理解两者之间的关系，还需要引入其它三个概念：errors in inferential decision（推断决策中的错误）、power of analysis （检验效能）、strength of relationship 或effect size（关系强度或效应规模，注1）。

我们从统计显著性开始，因为大家在看一个统计分析（如相关、回归、方差等）的结果时，总是首先看其显著性（即p值是否小于预设的α值，如 0.05），然后据此而做出相应的推断决策。如p<α则拒绝零假设、p>α则接受零假设。大家知道，尽管有上述p值做依据，这种决策还可能含有误差。如当p<α时，也许零假设还是对的，这时就有犯概率为p的Type I error（型一或“拒真”错误）。相反，如当p>α时，也许零假设却是错的，这时就有犯概率为1 - p的Type II error（型二或“纳伪”错误）。相信大家都看过这些老套的话，但也许不知道这些老土道理是解决很多困惑（包括丁丁的问题）的基本原理。

丁丁关心的是在大样本条件下犯型一错误的可能性。我们先看一下他（她）的例子：有两个均值，分别为3.7和3.5，各自的标准差均为1.0，由于不同样本量而出现了以下两种情况：

一、当N = 100时，两个均值的联合标准误差 = = 0.14（注2），检验两个均值之差的t = (3.7-3.5)/0.14 = 1.41，其相应的p = 0.160（注3）。

二、当N = 200时，两个均值的联合标准误差 = = 0.10，检验两个均值之差的t = (3.7-3.5)/0.10 = 2.00，其相应的p = 0.047。

可见，随着样本的增大，原来不显著的差别现在显著了，这合理吗？就型一错误而言，完全合理。当N = 100时，如果我们拒绝零假设（即3.7 = 3.5），拒真（“真”= 零假设）的风险由16.0%，太大了，不能容忍；而当N = 200时，拒真的风险降为4.7%，在可以容忍的范围内，所以是合理的。

那么，统计上显著的就一定是实际上重要或有意义的吗？自然不是。问题是我们如何判断一个统计显著的结果是重要或有意义？丁丁想知道的大概就是这种判断根据。这种根据，就是我们说的关系之强度或效应之规模（而不是样本最大量问题）。

判断关系强度或效应规模的一个直观（即非正式）准则是两个均值之差要大于均值的十分之一（注4）。如在本例中，均值之差为0.2、远小于均值的十分之一（0.35或0.37，取决于我们以那个均值为比较基准），显然，即使当N = 200时0.2的差别是统计显著的，但其差别还比较小（相对于均值的取值），没有特别的意义。

判断关系强度或效应规模，还有很多更正式的准则，如Pearson’s r（用于关系强度）或Cohen’s d（用于均值之差，注5），两者还可以互相转换（注6）。在本例中，Cohen’s d = 0.2（注7）。按照Cohen的说法，如果d值小于0.3，效应规模为small（小效应）、如果d值在0.5附近，效应规模为medium（中效应），而如果d值在0.8以上效应规模则为large（大效应）。

我们也可以将d转换成Pearson’s r = 0.1。一般说来，r = 0.1 也是一个弱相关。

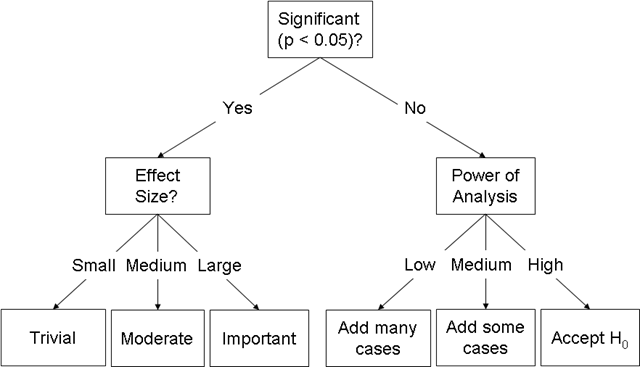
下图是对以上讨论的一个小结（包括丁丁问题的反面，即如果统计分析的结果不显著时，大样本有什么好处或坏处）。

 

上图也间接回答了丁丁最后引用的问题“统计学家可以证明任何事吗？”。是的，统计学家可以通过提高样本来拒绝零假设，但是，统计学家无法控制关系的强度或效应的规模。如何提高关系的强度或效应的规模？这既是一个理论问题、也是一个（数据收集）方法问题。本庄以前曾有涉及、日后有机会还会讨论，这里就不扯开去了。

注释：

注1：两者同义。关系强度多半用于相关或回归分析而效应规模多半用于方差分析。

注2：丁丁没有交代是两个独立样本还是两个非独立样本，我们假定是前者。

注3：双尾检验。p值可以根据给定的t值和自由度数，用Excel里的TDIST函数求出。

注4：所以一般说来，做社会科学研究的学生最好分别修一门专讲数据收集方法课和一（至数）门统计课。

注5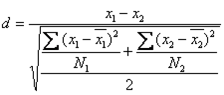：, 此外还有其它很多与Cohen’s d大同小异的计算均值之差的效应规模的公式。

注6：

注7：算了老半天，d等于均值之差，这是因为两个组的样本量相等，否则会有所不同或很不相同。