为何不同模型的路径系数和拟合度相同？

Anonymous @ 2009-08-31：

老师您好! 我也刚开始尝试使用SEM做中介效应分析,看了您的几个相关帖子,受益匪浅。恕我愚钝,还有几个问题不明白,还望进一步指教。

1). 您在"如何检验两个中介变量的效应"的帖子中提到：中介效应需要满足三个或者四个条件,其中包括:X或Z(自变量)对Y(因变量)的间接影响大于其直接影响（即 γAX × βYA > βYX 或 γBZ × βYB > βYZ ）。我不明白为什么一定要满足这个条件？如果是这样，是否意味着中介模型中间接效应都大于直接效应，或者说中介效应的比例大于50%。可我经常看到一些文献说，某某变量的中介效应比例为多少多少（低于50%），难道这是错误？

2). 最近我也做了一个中介效应的模型，概念模型类似于6月30日“如何在模型拟合度和模型合理性之间选择？”帖子中的模型。首先用软件跑了模型1，所有系数都显著，模型的拟合度也可接受；接着跑了模型2，结果是所有路径系数也都显著，模型也可接受。我不理解的问题是：a.两个模型不一样，为什么拟合度都可接受；b.两个模型种，W和Z到X的路径系数尽然完全一样，模型都不一样了，怎么路径系数还会相同？其中，X到Y的系数，模型2要比模型1小？C.模型2中，数据显示 βwx * βxy < βwy ,请问这还存在中介效应吗？

不好意思，一下子问了好多问题，也许许多问题还非常初级，见笑了。不慎感激！

庄主 @ 2009-09-05:

1). 为了理解你的问题，我重读了一项原文，发现其中的直接影响符号写错了（现已改正），应该是γ_YX和γ_YZ或而不应该是β_YX和β_YZ（图中的符号是对的）。也就是说，你问题中提到的为何“γAX × βYA > βYX 或 γBZ × βYB > βYZ” 应该是“γAX × βYA > γYX 或 γBZ × βYB > γYZ"。（当然，你对原文的理解没有错。）

我在原文中说过，严格的中介效应模型要求直接影响（即γYX 或 γYZ）彻底消失。这时，间接影响（γAX × βYA或 γBZ × βYB）自然大于直接影响。如果直接影响不等于0但小于间接影响，那么可以认为这是一种让步或妥协的微弱版（weak version）。如果再推一步，直接影响不但不等于0而且大于间接影响，那么直接影响是主流或中心路径(central route)、间接影响只是支流或边缘路径（peripheral route)，那么中介效应的原始意义就大大打折扣了。这是一个理论问题、不是纯粹的统计问题（意思是，间接影响还存在，但没有必要强调其涉及的“mediation process”了）。

我还没看到过你提到的"中介效应的比例大于50%"，是指间接影响的值至少为直接影响的值的一半吗？如果这样，那是对上述微弱版的进一步弱化。

2a). 你的两个模型不同（模型2多了四个系数、少了四个自由度）、但拟合度都可以接受的现象很正常和普遍，因为各自检验的零假设相同，都是模型与数据之间没有显著差别。但是，你还要检验一个零假设，就是两个模型的拟合度之间没有显著差别：如果两者确无差别（即由于增加了间接影响而提高的误拟合度被损失了的自由度所抵消了），则说明间接影响（即中介效应）并不显著；反之则说明存在显著的间接影响（中介效应）。

2b). 你问“两个模型中，W和Z到X的路径系数尽然完全一样，模型都不一样了，怎么路径系数还会相同？”其中的W从何而来？估计你将我另一帖了的符号（其中也许W和Z是自变量、X是中介变量）混着用了。但是如果是这样的话，X不应出现在模型1.而你却说“X到Y的系数，模型2要比模型1小”相矛盾。难以理解。最简单的方法是提供两个表格，一是模型1的变量及其系数、二是模型2的变量及其系数。

2c). 你问的就是：当一个间接影响小于直接影响时，是否还有必要和价值讨论中介效应？我上面已经讨论过。按经典的定义和学术界的主流看法，至少是意义不大。

如何理解“中介性模型是一个因果模型"?

z @ 2009-08-31:

我的研究假设包含一个中介变量而我的数据来自一次性调查(one-shot survey)，我用SEM分析，结果拟合的很好。但审稿人批评说，虽然模型拟合了，但并没有证明该模型的因果关系，如自变量先于中介变量、中介变量又先于因变量。

我在“中介关系之父”David Kenny的网上(http://davidakenny.net/cm/mediate.htm)读到一句话“a moderational model is a causal model”（“中介性模型是一个因果模型”）。是否可以用来为自己辩护？

庄主 @ 2009-09-05:

恕我直言，你对Kenny的理解，可以说是典型的断章取义。以下是他原话的完整段落：

“Note that a mediational model is a causal model. For example, the mediator is presumed to cause the outcome and not vice versa.  If the presumed model is not correct, the results from the mediational analysis are of little value.  Mediation is not defined statistically; rather statistics can be used to evaluate a presumed mediational model.  The reader should consult the section below on  Specification Error.” （“中介性模型是一个因果模型。例如，假定中介变量影响因变量而不是反过来。如果这种前提假定并不成立，那么中介分析的结果就是毫无价值的。中介影响不能通过统计分析来证明，统计分析只能用来检验以中介性为前提的模型。读者应该参考以下有关模型设定中的错误。”）

相信你一定学过因果关系的三项条件：自变量和因变量之间具有相关性；两者的产生又有先后之别；不存在导致这种因果关系的其它变量。在中介性模型中，这三项条件需要扩展一下：自变量(X)和中介变量(M)之间、中介变量和因变量(Y)之间各有相关性；三者之间的产生又各有先后之别(X->M和M->Y)；不存在导致这种因果链(X->M->Y)关系的其它变量。

Kenny的话指的是在上述条件二存在的前提下，SEM或其它统计分析方法可以检验条件一（甚至条件三，如果你的模型中包括了“一切可能的第三者”）的合理性。如果条件二不存在（如一次性调查数据）的话，拟合得再好的SEM也只证明了X和M之间以及M和Y之间的相关、并没有证明X->M->Y的先后次序。也就是说，哪怕X和M以及M和Y各自高度相关，三者之间的因果链还有X->Y->M、M->X->Y、M->Y->X、Y->M->X、Y->X->M等五种其它可能性！

如果你继续读一下Kenny有关“模型设定中的错误”一节的话，就会知道他在那段的开始还在强调上述（我演绎）的思想：

“Mediation is a hypothesis about a causal network.  …  The conclusions from a mediation analysis are valid only if the causal assumptions are valid.”（“中介影响是一种有关因果网络的假设。 … 中介分析的结论只有在有关因果条件存在之下才能是正确的。”）

还是那句老话，变量之间的因果次序是由数据的采集过程来决定的、而不是由统计分析（包括SEM）来决定的。

如何在EViews或Stata里计算Finsher转化值？

旭 @ 2009-07-23：

祝老师您好！我是一个学经济学的学生，目前正在做毕业论文，是关于跨国GDP与消费之间相互关系的研究。看了您的“如何检验两个相关系数的差别？”一文，感觉受益匪浅，帮助很大。因为这就是我要做的东西：把各国之间GDP与消费增长率的相关系数算出来，然后把对应的GDP与消费增长率的相关系数（如中美之间GDP增长率的相关系数和中美之间消费增长率的相关系数）做费雪转化，求出Z值看他们之间的区别显不显著。在文章里您给出来算费雪Z值的一个EXCEL公式，可以算出结果。但是我的导师说EXCEL不是一个ACCEPTABLE统计软件，让我用EVIEWS或者STATA软件做这个结果，想请教下您，能不能在这两个软件里做上述分析结果呢？如果可以，该怎么做呢？

庄主 @ 2009-08-30:

任何软件只要其公式一样，结果应该是一样的，不存在高贵低贱之分。我曾说过，SPSS是傻瓜机而Excel是智能机，因为前者一般只报告计算结果而不显示计算步骤，而Excel是让你自己一步一步算出结果。就这意义上说，其它统计软件（包括EViews、Stata、SAS等）也是傻瓜机。当然，就本案的如何计算Fisher z-transformation而言，我在原文中教大家的是直接套用Excel提供的函数FISHER()，那也是一个傻瓜工具。但你也可以根据我原文中的公式

 

写出如下的Excel计算公式：=0.5*LN((1+A2)/(1-A2))

注，其中“A2”是你的相关系所在格。你也可以先用函数求、再用手工来验证。难道这样的结果还不acceptable？

如果一定要用高贵的EViews、Stata或其它软件来计算，道理一样。首先，你要建一个新文件，将你的相关系数作为一个变量放到一个column里，然后写一句类似上述Excel公式的指令，如

F = 0.5*LN((1+R)/(1-R))

其中F是转换后的值，R是原始相关系数。我手头没有EViews和Stata的手册，不知它们是有LN还是其它符号来代表自然对数函数。

再次呼吁：同学们大家起来，不要做统计软件的奴隶！

如何解读一个交互影响显著而简单斜率不显著的回归模型？

Anonymous @ 2009-07-30:

Hi, Dr ZHU, I may want introduce myself first, I am a Phd Candidate from your university majoring in xxx (EDITED BY 庄主). I find your forum by accident and I have read some reviews on it, I really feel it is a good place to know more statistics knowledge.

I want to ask one question about the interaction effects of two independent variables (or we may also can say the moderating effect of one independent variable and one moderator, I may name them "A" and "B") on one dependent variable (I may name it "C"). I first use the traditional method, OLS- multiple linear regression in SPSS to run the produced term A*B's effect on C, I got a significant result, the T value is around 2.2 thus the P<0.05.

Then I further explore the internal mechanism of the interaction effect by using Cohen and Cohen (1983), Aiken and West (1991) and Dawson and Richter’s (2006) Simple Slopes Test [this method is designed for interpretation of the interaction effects of two continuous predictor variables, by this way one could interpret the significance level of the causal relationships between independent variable and dependent variable under high or low level of the moderator. To illustrate and test the significant interaction effects, separate regression lines were computed, plotted, and tested with one standard deviation below the mean on the moderating variables as well as one standard deviation above the mean of them.], this time I find the causal relationship between A and C is insignificant both under high B and low B level, in fact the coefficients take the opposite direction. Under high B level the coefficient between A and C is negative but insignificant, under low B level the coefficient between A and C is positive but insignificant.

I originally explain the significant moderating effect is: although under both high and low B level the causal relationship between A and C is insignificant, but because of the opposite coefficient, thus the moderating effect (A*B) may still be significant. But current one famous professor rejected my explanation; he told me that the results were inconsistent: 1. from one side, the moderating effect is insignificant. 2. form the other side, both under high and low B level, the causal relationship between A and C is insignificant thus can be treated as no relationship. How can you say them taking moderating effect first and later told us the effects were equal (A and C have no relationship) under both conditions (high and low B level)? Thus I am a little confused, as you know, in many cases, run the linear regression will meet such question as I described, so commonly how can we explain this phenomenon to cope with the journal reviewers' critique on this issue?

Many thanks!

庄主 @ 2009-08-29:

Thanks for the detailed explanations of your question.  It’s satisfying to know that someone of my own institution also reads this blog. Sorry for the delayed response as I’ve been traveling in the summer. To benefit other readers who might not be efficient in English, please allow me to reply in Chinese.

先简单回顾一下你的问题。你有模型1

C = b₀ + b₁A + b₂B + b₃AB                       (1)

其中A、B和C都是定距变量。你用OLS回归检验，发现b₃（还是b₁或b₂？）的t值 = 2.2 (p < 0.05)，即AB对C有显著的交互影响。为了进一步理解这种交互关系的“内在机制”，你采用了Cohen & Cohen等推荐的“简单斜率检验法”(test of simple regression slope)，即根据模型1的结果，将B的均值±1个标准差的值（分别记为B_H和B_L）代人模型1，来算出以下两个简单回归模型的斜率：

C = b₀ + b₁A + b₂B_L+ b₃AB_L = (b₀ + b₂B_L) + (b₁+ b₃B_L)A             (2)

和

C = b₀ + b₁A + b₂B_H+ b₃AB_H = (b₀ + b₂B_H) + (b₁+ b₃B_H)A           (3)

说明：因为B_H和B_L均是一个常数（而原来的B是一个变量），所以它们代入模型1后而得到的模型2和3，经过整理以后，都成为只含自变量A的一元（或简单）回归模型，而模型2中的b₁+ b₃B_L和模型3中的b₁+ b₃B_H就是你说的的简单斜率（就是我用蓝色标明的部分）。这时，你发现模型2的简单斜率b₁+ b₃B_L成了负值而模型3的简单斜率b₁+ b₃B_H仍是正值。你进一步对这两个斜率作了显著检验，发现两者均不显著。你的结论是“虽然A在调节变量B的不同条件下对C都没有显著影响，但是A和B的显著交互影响仍然存在”。但是，一位著名教授不同意你的说法，理由是：一、你的交互影响不显著（我不理解这句话，因为它与你说的模型1中的t = 2.2有矛盾）；二、A在B的不同条件下对C的影响都不显著。（不知我的上述理解是否有误？）

好了，现在谈谈我的看法。

首先，我有两处不清楚：一、如我已在上面问过，模型1中显著的是b₃还是其它系数？二、你还没有提到，模型1中的A、B和AB是否为各自的centered values（“取中值”，以避免或降低AB与A、AB与C之间的相关程度）？鉴于你已读过Cohen & Cohen, Aiken & West等经典文献，应该熟悉检验交互影响的基本步骤，所以我的回答是基于以下假定的：一、你说的模型1中t = 2.2的显著系数是b₃；二、模型1中AB与A、AB与C之间并不相关（这点很重要，不然、假定一是没有意义的）。

如果上述两个条件成立，那么你的A和B在样本中对C就是确实具有显著的交互影响。当然，因为你的t值接近临界值（1.96或更大），AB的交互影响应该是marginal（相当勉强）的，所以要审慎对待，至少要检查一下A的数据中是否存在异常值；如有异常值，则需要剔除后再次检验模型1，看看AB的影响是否继续保持显著，已确保该模型的robustness（“鲁棒性”）。

你的主要困惑（也是你教授理由之二）在于：为什么在模型1的b₃显著的前提之下，模型2和3的斜率不显著？这里存在一个许多教科书上没有明确解释、但初学者往往容易误解的事实，即AB之间的显著交互关系只是说明自变量(A)对因变量(C)的主影响(main effects)将随着调节变量(B)的取值而变化，但并不保证在B的不同取值上A的所有主影响都是显著的（但至少有一个取值上A的主影响是显著的，否则AB不可能显著）。用英语说，A significant interaction effect ensures not only the main effect of an independent variable on a dependent variable varies across different levels of a moderator variable, but also at least one of the main effects is significantly different from zero. However, the significant interaction doesn’t guarantee all main effects of the independent variable on the dependent variable to differ significantly from zero. 我们很容易用以下的图示来说明这个道理。

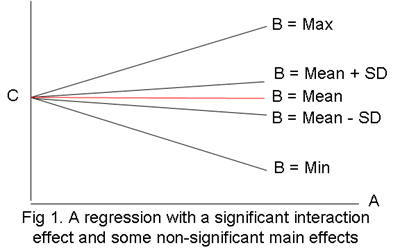
左图是我随手画的，其中有五条回归线，但都是根据同一模型（如你的模型1）而取B的最大值(Max)、最小值(Min)、均值(Mean)、均值减一个标准差（你的模型2）、均值加一个标准差（你的模型3）而画出的。虽然没有实际数据，但可以大致猜出五条回归线所依据的模型1的b₁和b₃的取值范围，即b₁（即A的总斜率）应该等于0，b₃（即AB的交互影响）则明显大于0（因为A对C的影响是放射的、即随着B的增加而增加）。当然，我们并不知道（也无必要知道）b₀和b₂的取值范围，因为它们与本案毫无关系。

图中B=均值的回归线显然是一条水平线，所以是不显著的(即斜率等于0)。而B=均值加/减标准差的两条线，虽然并非水平线，但也很接近，考虑到各自的抽样误差（注意，不要与标准差相混淆了）而其斜率与0没有显著差别（也许你的数据就是这种情况）。但是，B=极大值/极小值的两条线的斜率显然不等于0。如果我们再添加B=均值+/-2个标准差的两条线，可以想象它们的斜率也会不等于0。结论：当A和B对C有显著影响时，A对C的影响随着在B的取值而变化，有些显著而有些可能不显著。

以上是直观的解释。我们还需要略正规一点地总结一下。回到模型2和3，注意其中的蓝色部分（即各自的斜率）。它们是否=0，是由下述公式来检验的：

 

 

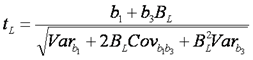
和

其中Var_b1和Var_b2分别是b₁和₂的方差、Cov_b1b3是b₁和₂的协方差。我们略过如何计算系数的方差和协方差的技术细节，而来看一下如何使得t_L和t_H达到显著水平（即大于2）。不言而喻的是分子要大而分母要小。就分子而言，从表面上看b₁、b₃和B_H或B_L三者均要越大越好，但更重要的是要三者取同样方向，否则会互相抵消（这不容易做到，尤其是当数据经过中心化处理之后，B_L一定是负的，而b₁或b₃的方向也会因A或B的中心化而与原始数据的方向相反）。而且，调节变量的取值(B_L或B_H)也不是越大越好，因为同时也会扩大分母。结论：t_L和t_H的取值受到很多正反因素的影响，很难做到永远显著。但是，这与b₁是否显著没有一一对应关系。

最后，你问如何使得期刊的reviewers接受你的解释。是的，有些（如果我用“很多”的话，大家可能会觉得我太狂妄，但是事实上“有些”不是一个小数目）reviewers也会将交互影响等同于主影响，所以你不仅要自己弄得很清楚，而且要说得很明白易懂，这时，公式和图表就是必要的辅助工具了。如何写好交互影响的报告，确是一个挑战。多读几遍Cohen & Cohen吧（他们的第三版就邀Aiken和West加盟合写了）。