为何两个模型的中介变量系数一样？

tan @ 2009-09-14:

祝老师,您好!这个星期的提问我看您都回答了,除了我提的问题。不知是您没注意到还是问题太初级而不值得回答。由于学识粗浅并确实想知道问题的解答，特此再次提问，烦请老师您或其他有识之人给予解惑。

问题是有关用SEM检验中介效应的：变量W和Z为自变量（且W与Z之间没有显著的相关），Y为因变量，X为设想中的中介变量。首先是模型1，只涉及三条路经：W--X；Z--X；X--Y。所有路经系数都显著，模型的拟合度也可接受；接着是模型2，涉及五条路：W--X；Z--X；X--Y；W--Y；Z--Y，即模型2比模型1多了两条路经（W--Y；Z--Y），结果也是所有路经系数都显著，模型的拟合度也可接受。我不可理解的问题是：在模型1和2中，自变量（W和Z）与中介变量（X）的路经系数竟然一样，怎么会这样？但模型1中X--Y的路经系数要大于模型2中X--Y的路经系数。

在此，我想请教的问题是：（1）上述模型（1和2）中，W和Z与X的路经系数有没有可能一模一样？在理论上成立吗？我担心在那个地方做错了。（2）根据您的几个帖子以及其它相关资料，中介效应并不是比较上述我所表述的两个模型的，但在我所学习的Marketing领域，有文献（作者还有一定的名气）却又是这样做的，特别提到：模型2拟合度可接受，所有路经关系都显著，故部分中介效应显著。这样做可以吗？再次感谢！

庄主 @ 2009-09-20:

上周有好几人提了问题，但我没有时间回答所有人的问题，只能按我对问题价值的判断而选择回答部分。我初看你的问题，觉得与8月31日匿名者提的问题相同（见为何不同模型的路径系数和拟合度相同？）。我现在还是这么认为（即，即使不是同一人问的，道理一样）。考虑到读者中也许还有同样的问题，所以再说几句。

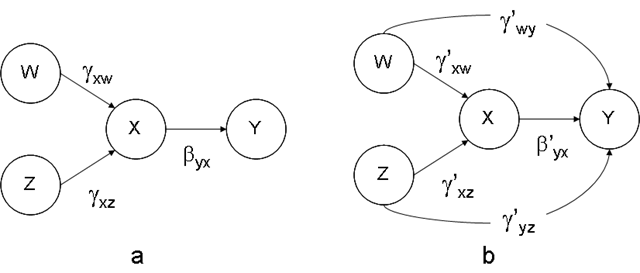
为了便于讨论，我将你的两个模型画了出来（建议：很多时候一图胜千字、但这里的提问处不让上传图像，请大家讲图贴在自己的博客或其它公共空间上，然后在你的问题中做个链接）：

问题一、“上述模型（1和2）中，W和Z与X的路经系数有没有可能一模一样？在理论上成立吗？”是否指λ_xw = λ'_xw和λ_xz = λ'_xz？如是，答案是肯定的。一个回归方程的系数当且仅当方程增减自变量时才可能变化。以本案为例，模型a涉及以下两个方程：

X = λ_xwW + λ_xzZ                           (a1)

Y = β_yxX                                      (a2)

而模型b也涉及两个方程：

X = λ'_xwW + λ'_xzZ                         (b1)

Y = β'_yxX + β'_ywW + β'_yzZ              (b2)

如果比较方程a1与b1，可见两者含有同样的自变量（W和Z），所以λ_xw一定等于λ‘_xw，λ_xz也一定等于λ_xz。（注：这是回归分析的基本原理，同样适用于SEM。）

问题二、“模型1中X--Y的路经系数要大于模型2中X--Y的路经系数”。比较方程a2和b2，可见b2比a2多了两个自变量（W和Z），因此β_yx可能不等于β’_yx，条件是(1)W或Z与Y相关（即β'_yw ≠ 0或β'_yz ≠ 0）和 (2) W或和Z与X相关（即λ‘_xw ≠ 0或λ‘_xz ≠ 0）同时成立。既然现在β_yx > β’_yx，说明W或Z两者之中至少一个与X和Y同时相关。（注：这也是回归分析的基本原理。）

问题三、“模型2拟合度可接受，所有路经关系都显著，故部分中介效应显著。这样做可以吗？”模型b的拟合度一定比模型a好，但是由于损失了2个自由度，所以要做统计检验以证明模型b与模型a之间有显著差别。如是，说明模型b更可取。但是，仅比较模型a和模型b而不比较模型b与只含W->Y和Z->的“直接影响模型”（参见如何检验两个中介变量的效应?），确实不是检验中介效应的充要条件 (necessary and sufficient conditions)。为何你们marketing中有“一定名气”的作者这么做？我无法回答，我只知道科学面前人人平等。包括我在内的很多人都相信David Kenny的检验中介变量方法，不是因为他名气大，而是觉得他说的有道理。