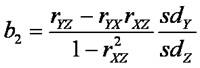如何处理严重的缺省值问题？

L @ 2010-10-11:

您在博客中讲解如何报告回归分析时，提到：“但变量常有缺省值，这时模型的个案数就会小于样本数、有时两者相差很大（当然是个严重问题），所以一定要报告前者。”

我在处理一批调查数据，遇到了严重的缺省值问题。我的样本有近千人，用媒体使用的三个自变量和三个人口控制变量（简称X1-X6）对因变量（简称Y）做回归分析，只剩下300个案。请问对此如何处理。

庄主 @ 2010-10-13：

数据缺省值是定量研究者人人遇到都头痛的问题。因为缺省值就是数据里没有信息，巧妇难为无米之炊。

我看了你的数据，主要问题在于X1-X3等3个变量上的缺省值太多（各有200-400个缺省值不等）。如果去掉这三者，会有600余人个人留下来，大概可以接受。但是，这三个自变量是你研究的核心变量，如果删掉它们而只留下3个人口控制变量，也就难以成为传播学研究了。真是一个两难问题。

现在流行一种“Missing Value Analysis“(MVA，即“缺省值分析”)，SPSS下属的结构方程模型软件AMOS中就有MVA工具。其基本思想是根据已知信息去预测（即填补）缺损信息。具体操作步骤如下：

1. 假定样本数据中有十个变量（已经用于回归分析的X1-X6和Y，以及没有用上的Z1-Z3），先把Y放一边，分别分析其中八个变量与第就个变量之间的关系。即：

X1 = b0 + b1X2 + b2X3 + b3X4 + b4X5 +b5X6 + b6Z1 + b7Z2 + b8Z3             (1)

X2 = b0 + b1X1 + b2X3 + b3X4 + b4X5 +b5X6 + b6Z1 + b7Z2 + b8Z3             (2)

X3 = b0 + b1X1 + b2X2 + b3X4 + b4X5 +b5X6 + b6Z1 + b7Z2 + b8Z3             (3)

注意，这里每个模型的有效样本数为该模型所有九个变量（包括因变量Y和八个自变量）上都没有非缺省值的个案数。在你的案例中大概是600多人。

2. 根据模型1-3的结果参数（即b0-b8）来分别预测X1-X3上的缺省值。假定模型1的结果是：

X1’ = 0.5 + 1.0X2 + 1.5X3 + 2.0X4 + 2.5X5 +3.0X6 - 2.0Z1 + 3.0Z2 + 1.0Z3    (4)

那么，就可以根据那些在X1上有缺省值的个案的X2-X6和Z1-Z3的实际数值而预测出（填补进）他们在X1上可能取的值（记为X1’）。同理，可以预测出X2或X3缺省值的可能取值（分别记为X2’和X3’）。

3. 最后将填补后的X1-X3（即X1’, X2’, X3’）放回你一开始想做的回归模型，即

Y = b0 + b1X1’ + b2X2’ + b3X3’ + b4Z1 + b5Z2 + b6Z3                                  (5)

MVA是否合理和有效，取决于以下三个条件能否同时被满足：

一、每个模型中的所有就个变量上上没有（或是很少）缺省值，否则“救”不回多少个案。假如每个变量有30个缺省值（即只占样本的3%），看来微不足道，但是如果每个变量上的30个缺省值发生在不一样的个案上，那么就有30X9=270个案无法就回。

二、每个模型有一定的解释力（如R平方在0.20以上，当然越高越好），这决定了用该模型中八个自变量去预测Y的validity（效度）。

三、每个变量上的缺省值是完全随机(completely random)产生的，即不受任何规律制约；不然，必须将影响缺省值产生的因素放进模型中去。

以上条件一和二是可以从已有数据中计算出来的。如果一和二无法成立，那么就则是彻彻底底的无米之炊了。如果条件一和二问题不大，那就需要看条件三了。

条件三一般是无从得道的。不过根据前人研究（包括我自己做过的一个大型研究），缺省值的发生一般都不是完全随机的。也就说，使用MVA在大部分情况下都是有风险的。缺省值产生的随机性越低、用MVA的风险就越高。

以上是现有文献中对MVA的基本看法。此外，我个人觉得用数据中除了因变量之外的所有变量来预测缺省值的做法有totalogy（自我循环）之弊端。以本案为例，你比较一下模型4与模型5，就不难看出Z1-Z3对Y的影响出现了四次：一次是自己的直接影响（模型5）而另三次是分别通过X1’、X2’和X3’的间接影响。这在理论上和方法上都有问题（如X1’-X3’与它们的预测值Z1-Z3之间有共线性）。

我认为，解决上述问题的一个办法是将Z1-Z3从模型1-3中去掉。就是说，只用模型5之外的变量来预测X1-X3的缺省值。如此填补出来的X1’-X3’在模型5中与Z1-Z3应该没有过高的共线性；同时，Z1-Z3对Y的影响只被估计一次。当然，这种方法并无法解决X1-X3中缺省值非随机产生的问题。

最后还是那句话，缺省值就是数据中缺乏信息。MAV或其它任何统计方法（包括我提出的改进方法）都无法根本解决信息不足甚至信息匮乏的问题。

如何判断各项选择之间是否存在独立关系？

张君 @ 2010-08-31:

老師: 您好! 我來自台灣，姓張。看了老師許多的文章，讓我受益良多。在此有個統計上的問題，想要冒昧請教：如果我要研究的依變數為多分類（多於二分類），各類之間又沒有順序時，我是否該用multinomial logistic model來加以分析？但是，如果我的依變數各分類之間的關係為不獨立時，是否就該改用別的model?

舉例來說：我想研究什麼樣的學生會選擇什麼樣的交通工具去上課時,依變數是一個三分類的變數,選項分別為搭紅色的車,搭藍色的車以及不撘車。如果用multinomial logit的話，IIA檢定是一定每沒辦法過的；改用multinomial probit的話，在理論上又好像不太對。由於學生們的選擇在理論上來說應該是先選擇搭不搭車,再來選搭紅色或搭藍色的車,所以我是不是應該各別跑一個二元logit模型呢？第一個分析搭不搭車，第二個分析搭藍色或紅色。還是有其他更好的方法可以做更直接的分析，就請老師多多指教了。

庄主 @ 2010-09-04:

很抱歉，我对IIA 假定（Independence of Irrelevant Alternatives，不知你们是如何译成中文的？）知之不多，没有做过任何第一手的研究。以下只是根据直觉来谈谈，不要太拿我的话当一回事。

从有关文献来看，我觉得IIA假定是一个相当理想化的状态。就是说，各种选择中的 irrelevant alternative(s)（“无关选项”？）是真正无关或独立的。然而，这种理想状态大概只能在实验条件下才会出现。而在实际生活或实际研究中，很难会有真正的独立选项。（我对台湾不太了解，但一直好奇：2004年大选，如果没有第三党候选人，结果会一样吗？）

如你的“红车、蓝车和不搭车”问题，大概也只是一个举例，你的实际数据应该更复杂一些。

简言之，多项选择之间的关系，应该是一个理论而不是统计问题，需要根据具体的研究问题来确定。如果没有明确的理论指引，我个人倾向将各项选择看作是相关事件的竞争关系（我自己的很多研究课题都是根据zero-sum原则来展开的）。当然，你可以同时用两种或多种方法分别分析一下，看看各种结果之间有多大差别？那种方法的结果看上去更合常理？

如何检验两个模型拟合度的差别？

Anonymous @ 2010-09-01:

祝老师您好！我看了您对“为何不同模型的路径系数和拟合度相同”一文的回复，有一处不明白。想向您请教。即，当两个模型对同一组数据的拟合都可以接受时，如何检验这两个模型的拟合度之间有没有显著差异呢？

庄主 @ 2010-09-02:

首先要分清这两个模型之间是否具有从属关系。如果是的，可以用常规的模型比较方法来检验；否则需要用非参数的统计量。下面分别说一下。

主从关系模型之比较

什么是模型之间的主从关系 (hierarchically nested)？如果两个模型（A和B）具有相同的变量（包括隐含因子和观测指标）、而其中模型B是在模型A的基础上减去若干参数，这两个模型就被认为是有主从关系。按参数的个数来看，模型A是主（full model）、模型B是从（reduced model）。请看以下例子：

上图中，A和B在measurement model（测量模型层面）上完全相同；但在structural model（结构模型层面）上则不同：在A中因子X对因子Y有直接影响（记为g2），而在B中X对Y没有直接影响（也即g2=0）。这两个模型之间就是具有上述的主从关系，所以可以直接用常规的模型比较方法对两者之间的差别进行显著性检验。

所谓“常规的模型比较方法”，是指计算两个具有主从关系的模型的卡方值（分别记为χ_Asup>2和χ_Bsup>2）之差（记为Δχ²），然后根据两个模型的自由度（分别记为df_A和dfχ_B）之差（Δdf），从卡方分布表中查出该Δχ²），所对应的显著水平（p-level）。

以上图中的模型A和B为例。假定A的χ_A² = 150.0而B的χ_A² = 145.0，Δχ² = 150.0 - 145.0 = 5.0，而df_A = 22（这不是假定而是实际的，因为该数据有45个已知值、23个参数；大家可参照前贴如何计算SEM中的自由度？来计算本例各模型的自由度）、df_B = 23（很显然，因为B少用了一个参数、因此多一个自由度）、Δdf = 1。根据卡方分布表（可参考以下http://www.fourmilab.ch/rpkp/experiments/analysis/chiCalc.html），如果df = 1而χ² = 5时，其对应的p-level = 0.0253。那么，我们的结论是什么呢？即，A和B之间是否有显著差别呢？或者，在A和B之间我们应该选择哪个呢？请大家自己得出结论。如果有疑问，请继续提出。

非主从关系模型之比较

如果两个具有同样变量的模型之间没有上述的hierarchical nested关系，就无法直接比较了。上图中，A和C也是有主从关系的，但B和C却不具备主从关系，尽管两者都是A的从属。两个非主从关系的模型之间的比较，一般是用Akaike Information Criterion (AIC)或类似的非参数统计量（non-parametric statistics）如Bozdogan's Consistent AIC (CAIC)或Browne-Cudeck Criterion (BCC)。所谓“非参数统计量”是指该统计量的概率分布（也就是说其显著性水平）是个未知数。所以比较两个非主从关系的模型之间AIC（或其它）的差别，我们只能知道其中那个模型对数据的拟合更好一些、但不能确定这种差别在总体里是否存在。

以上图的B和C为例，假定AIC_B = 120和AIC_C = 135，我们可以知道B对数据的拟合更好（因为AIC及其它类似统计量都是越小越好），但是我们无法得知ΔAIC = 15的p-level是什么。因此，非主从关系的模型之间的比较，只是非正式的研究。

如果一定要检验两个非主从关系模型之间差别的显著性，那就需要找到一个B的替身（且称为B’)，其即同时为B和C的主模型、但又与B没有显著差别。在本例中，A是B和C的主模型、但是与B有显著差别，所以不能承担B的替身。如果能找到B’，那么B’与C是主从关系，就可以按上述的常规模型比较方法来检验B’与C的差别了。

如何处理SEM模型中的“坏”因子？

SJ @ 2010-05-17:

我是X大学心理系的学生，目前在美国Y校访问。最近在处理数据时遇到问题不知该如何解决，之前在您的网页上冒昧向您请教过，非常感谢您当时的回复。我后来找了一些相关的文献看，知道了多组比较的大概步骤，但在统计中又遇到了新的问题，所以再次向您请教。谢谢您关注我的邮件！

我探讨的是暴力游戏对青少年攻击性影响的性别与年龄差异。研究变量包括：

• 自变量：玩暴力游戏的程度(VVG -- 庄主注，下同)
• 因变量：身体攻击(Physical Aggression)
• 中介变量：信念(Belief about Aggression)、期望(Hostile Expectation)、移情(Empathy)
• 调节变量：性别、年龄

因此我把全部被试（795人）按年级和性别分成六个组，每组100多人，想比较不同性别、不同年龄孩子模型的路径差异（庄主注：这应该是一个moderated mediation模型，对此有兴趣的读者请仔细理解本案例的模型设置及有关讨论）。

比较结构模型前，为了确定测量等同(measurement invariance -- 庄主注)，我分别对信念、移情和身体攻击这三个潜变量进行了单组和多组的CFA。以因素负荷相等(factor loadings invariant -- 庄主注)为标准，最后确定了5项目的信念、5项目的身体攻击及12项目的移情测量，能够满足跨组测量等同。信念和身体攻击是完全等同，两个移情项目虽不等同，但考虑到12题中只有两题不等同，所以认为部分等同也能允许进入结构模型的比较。

上面我所提及的CFA是分别针对每一个变量（庄主注：应该是factor吧？）进行的。但当我把所有变量（庄主注：也是factors吧？）都整合到一个模型后发现，六组都不能很好地拟合总模型。我看了修正指数（modification index或MI -- 庄主注），发现问题主要出在移情这个变量上。在前面的测量等同阶段，我删掉了16个移情项目，保留了12个项目，这12个项目分属5个因子。在结构模型中，我把这个5个因子作为移情的指标（庄主注：Empathy成了一个second-order factor？），但发现指标间及指标与其他变量还存在复杂的关系，这导致了模型不能较好拟合。

我又尝试了很多次，尝试找到一个移情的测量模型（measurement model -- 庄主注），无论是单个变量的单组及多组CFA，还是放到总模型中时，都能拟合六组数据，但徒劳无功。

如果把所有变量都当成显变量，那模型都能拟合得很好。但我能这样做吗？如果把所有变量当成显变量来处理的话，那前面的测量等同检验是否还有必要？

我实在不知道该如何考虑和继续，所以冒昧请教，请您给予我指导，非常感谢！

附件的图是我在确定了各组的测量等同后，用总数据做的模型。我担心我说得不清楚，可能看看模型会有帮助。再次感谢！

X²(114) = 411.1, p < .001, RMSEA = .06, NNFI = .90, CFI = .91

Note: Unstandardized coefficients are provided first, with standardized coefficients in parentheses. All paths are significant.

SJ @ 2010-05-21:

在等待您的回复之余，我这几天仍然在尝试寻找拟合潜变量的总模型，但可恨NNFI仍徘徊在0.8几（如果拟合很差我也就放弃了）。我发现问题在于移情量表。因为当我把三个潜变量当中的移情视为显变量，保留攻击与信念作为潜变量时，模型的拟合是可以的。移情的四个子量表之间有复杂的关系，而这不是我这个研究想关注的问题。我该如何处理呢？

庄主 @ 2010-06-13:

正如我在你上面叙述中加注所说，你想研究的是一个moderated mediation (“被调节的中介效应”？) 模型。虽然这种模型有点复杂，但是你遇到的三个问题（见下），却是在其它各种模型中也经常会出现。

一、为何你对三个中介变量分别做CFA时各自都拟合得很好，但当将三个因子合在一起做CFA时却拟合不好？这很常见。一般而言，单个因子CFA（即只有一个因子的模型）非但没有意义、而且富有误导性。实际研究中，最简单的模型至少也有两个因子。而拟合任何一个多因子模型，则不但需要每个因子内部的测量指标之间高度相关，而且需要各因子之间的测量指标基本独立（见下图a）。而如果数据是下图b那样，则会出现单因子模型拟合很好而多因子模型拟合不好的现象。在本例中，如果分别拟合X1-X3和Y1-Y3，会得到两个很完美的模型，但那是假象，X1-X3和Y1-Y3实际上应该同时属于一个因子。

二、为何总样本的拟合度要比六个分样本的拟合度好？你没有这么说，而是我从你提供的总样本模型拟合度（应该是勉强可以接受）和对分样本结果的叙述（如“六组都不能很好地拟合总模型”和“NNFI仍徘徊在0.8”等）中推出。这应该与你的分组样本过小有关。如你所说，每个分样本100余人，而每个模型含30来个测量指标（（= 22个中介变量指标 + ？个自变量指标 + ？个因变量指标）。计算样本量是否足够的一种快捷方法（不一定精确但大体上可靠）是样本量除以测量指标数。文献中最宽松的说法是应该大于10（我倾向于更大一些）。而你这里只有4-5之间。样本小的一个直接结果是指标之间的相关程度不稳定（可以更高或更低）。回到上图，总样本容易接近a，而分样本则难。这里不怕因子内部相关程度变低，而是拍因子之间相关程度变高。

改进的方法包括：增加样本（你大概做不到）；减少分组（如两个年龄组 X 两个性别组 = 4）；减小测量指标数（尤其是“移情”用了12个指标，有必要那么多吗？）等。

三、“移情”是个“坏”因子，是否可以将其12个测量指标直接进入模型（即你说的“显变量”）？如果为了提高拟合度，当然可以这么做。但是，这在理论和统计上都是下策。首先，显变量都是含测量误差的；其次，一个含12个显变量作为中介变量的模型是无比复杂；再次，部分（或很多）显变量之间会有共线性问题；等等。所以，你得到了模型拟合度的改进，但失去了更多。

我并不了解你的“移情”量表之来历，估计是个已被前人验证的成熟（？）工具。如此，为何在本案中成为“搞坏了一锅汤的老鼠屎”呢？也许是问卷翻译的问题？或是被测对象的不同（文献中的移情是用于儿童的吗）？还是加在其它问题之后（？）产生的副作用？等等。可能有很多种原因。你说移情不是你本研究想关注的问题。但是，如果该因子的测量模型太有问题，那么，你只能在整体删去这个因子和显变量处理之间做出痛苦的选择。如果是我，会选择前者。

为何一个自变量在总样本和分样本中的显著性不同？

Anonymous @ 2010-06-02:

老师：您好。我在做回归分析的时候遇到一个问题，想向您请教。假设我用一些自变量解释因变量y

y=a0+a1x1+a2x2+...+anxn     (模型1)

最后得到的结果是x1(如非农收入比重)，x2(如政府补助)与y1显著相关(p<0.01)。我的指导老师希望我对样本进行分组，分为参与非农产业与未参与非常产业，然后对两个子样本分别进行回归分析。他想考察参与非农产业与不参与非农产业的情况下，x2对y的解释力是否有差异。得到两个模型：

参与非农产业的样本（样本2）：y*=a0*+a2*x2*+...+an*xn* （模型2）

不参与的样本（样本3）：y‘=a0’+a2‘x2’+...+an‘xn’ （模型3）

结果模型2里，x2与y之间显著相关，模型3里二者并不相关。我的指导老师就说这是因为，x2与y之间之所以显著，就是因为在样本2里二者有显著相关关系。对于不参与非农产业的样本，x2与y之间并无关系。因为我对统计知识一无所知，所以上来向老师求助。我的指导老师的说法对吗？出现这种结果还可能是什么原因？或者怎样理解这种现象？

期待您的回复，谢谢

庄主 @ 2010-06-05：

虽然你描述了很详细，但我还不敢肯定完全清楚你的数据（如Y是什么？）和以及你指导老师的意思（他的话“X2与Y之间之所以显著是因为两者有显著相关关系”好像是同义词重复？）。

我猜，你的核心问题是为什么X2在总样本和分样本1中对Y有显著影响，但在分样本2中没有显著影响？假定你是根据X1而将总样本一分为二的（因为X1没有出现在模型2或3中），那么X2只在分样本1中显著的原因有二：

一、X1与X2对Y有交互影响（interaction）。简单说来，X2对Y的影响不是一个常数，而是随着X1的值而变化，如当X1 > 0 (是吗？)时，X2对Y有显著影响；而当X1 = 0（是吗？），X2对Y并无显著影响。至于为什么会这样，则是需要用你们的专业知识来解释了。

二、由两个分样本的大小不同而造成。我们知道，相关系数或回归系数的显著性与样本大小直接有关。如果两个样本的大小不同，即使两者的相关系数或回归系数相同，其中大样本的系数可能显著而小样本的系数则可能不显著。这是一种方法上的artifact（即人为假象）。你需要检查一下两个分样本的大小是否相同。

事实上，如我在前贴（如“分样本比总样本的回归分析更准确吗？”）中指出，检查X1和X2的交互影响，不应该将样本按X1的值分成两个分样本来比较a2，而是应该在总样本（即你的模型1）中加入X1和X2的交互项（即X1和X2的乘积），用你的模型术语来表示，即为 Y = a0 + a1X1 + a2X2 + a3X1X2 + ... + anXn。其中a3的显著性直接检验了a2是否随着X1的变化而显著变化，并避免了因为将总样本分成分样本而造成的人为不显著假象。

如何比较自变量与中介变量的解释力？

YF @ 2010-04-19：

庄主，非常感谢您对学生的慷慨指导，我想向您请教一个新问题。《管理世界》上有篇文章（见以下出处），是研究中介效应的，其自变量是家长式领导方式，应变量是团队绩效，团队冲突管理方式。作者按照Baron & Kenny（1986）检验中介变量的方法，分析结果用表2表示。

我的问题和该作者文章没有关系，是以该文章为例：（1）如果比较中介变量和自变量对应变量的解释力是否有意义？（2）如果有意义，是否根据下表2结果可以比较中介变量和自变量对应变量的解释力？如果可以根据下表2结果比较，那么看哪两个数据？例如：如果比较仁慈领导和合作型团队冲突解决方式对团队绩效的解释力，是根据0.726**（model 3）〉0.513**（model 2），还是根据0.662**（model 4）〉0.126（model 4），认为仁慈领导对团队绩效的解释力大于合作型团队冲突解决方式对团队绩效的解释力。

文献出处：张新安, 何惠, 顾锋. 家长式领导行为对团队绩效的影响：团队冲突管理方式的中介作用. 管理世界, 2009, 3: 121-133.

庄主 @ 2010-04-21：

问题1：比较中介变量与自变量之间对因变量的解释力之差别，是否有意义？有，但这只是检验中介效应的规定动作之一。强度版的中介效应要求自变量（X）对因变量（Y）的直接影响（Byx）= 0 而其通过中介变量（W）的间接影响（RwxByw) > 0；而弱度版的中介效应则要求Byx < RwxByw。也就是说，Byx < Byw是中介效应的必要条件（因为Rwx小于1.0）。所以两者的差别是不喻而言的。如果Byx大于或等于Byw，那就没有必要再谈中介效应了。

问题2：如果比较Byx与Byw的大小，应该看模型4。你的困惑来源于作者不合适、也无必要用了四步的hierarchical回归（“分批进入回归”，参见我数贴中对在类似场合下使用这种方法的批评），模型2（自变量模型）和模型3（中介变量模型）的系数是不能直接比较的，因为模型2中的Byx是在Byw缺席情况下估算的，其中含有通过Byw的间接影响，所以是夸大了的；同样，模型3中的Byw的影响也因为由于Byx的缺席而被夸大了。只有两者同时出席的模型4才是直接比较的地方。

当然，模型2和模型3也有其用此，就是通过计算模型4的R平方 - 模型2的R平方（= 0.505 – 0.307 = 0.198）来得知两个中介变量（合作型和竞争型）对因变量的联合解释力，并通过计算模型4的R平方 - 模型3的R平方（= 0.505 – 0.478 = 0.027）来得知三个自变量（权威、仁慈、德行）对因变量的联合解释力。而表中模型2和模型3的ΔR平方则是没有什么意义的。由于很多读者对此有困惑，我再重复一下这种“nested testing”（嵌镶式检验）与上述“分批进入回归”的区别：

假定模型为Y = b0 + b1X1 + b2X2 + b3X3，分批进入回归的做法是估计三个模型，分别为Y = b0 + b1X1, Y = b0 + b1 + X2, Y = b0 + b1X1 + b2X2 + b3X3，然后认为：模型1的R平方代表X1对Y的解释力、模型2的R平方与模型1的R平方的差别为X2对Y的解释力、模型3的R平方与模型2的R平方的差别为X3对Y的解释力。其问题是模型1的R平方中包含了X2和X3的贡献、模型2的R平方中包含了X3的贡献。

嵌镶式检验是估计四个模型，分别为1：Y = b0 + b1X1 + b2X2 + b3X3（全模型），2：Y = b0 + b2X2 + b3X3（X1缺席模型），3：Y = b0 + b1X1 + b3X3（X2缺席模型），4：Y = b0 + b1X1 + b2X2（X3缺席模型），然后认为：模型1与2的R平方之差为X1对Y的独立解释力、模型1与3的R平方之差为X2对Y的独立解释力、模型1与3的R平方之差为X3对Y的独立解释力。这里的最后一步与分批进入回归的最后一步相同、但其它比较有数量和质量上的区别。注意，嵌镶式检验的三个R平方差其实就是模型1中X1、X2和X3的semipartial correlation，在SPSS中叫做“part correlation”，可以只估算模型1而得知，不需再分别运行模型2-4的。对初学者来说，分别操作一下有助于从理念上认识上面讨论的各种问题的逻辑。

如何绘制个人增长曲线图？

Z @ 2010-04-15:

我们有一3个wave的panel样本，用GLM Repeated Measures分析数据，并从中画出三个时间点上样本的平均值。我们写了一篇论文投给某国际期刊，有位评审人要求我们随机抽取10人，在同一图里显示各自的growth curves。我们在SPSS中试了很久，怎么也无法制作这种图。不知是否可以在SPSS中“自动”做到？

庄主 @ 2010-04-18:

最近我教的统计课里，也有一位同学提出相同的问题，其答案在于纵向数据的特殊结构。一般说来，纵向数据的结构有“矮胖型”和“瘦长型”两种。但你们需要的是第三种结构。

矮胖型数据与更常见的横向数据相似，每一列是一个变量、每一行是一个个案，由于纵向数据的因变量有多个时点的观测值，每个观察值被当做一个变量，分别占领一列，一般在因变量名后加下标1、2、…、t（t=时间点个数）来显示各自的观测时间点。所以，这种结构的正式学名叫做“multivariate format”（因变量多列型）。如表一代表你们的数据，其中Y1、Y2和Y3是因变量Y在三个时间点上的观察值，注意它们是被当做三个变量分别各占据一列，X是自变量（只测量一次，所以只有一列）、最后的“…”表示还可以有其它自变量。GLM、SEM等都是使用这种结构的数据。但是，这种数据无法用来制作“intrapersonal growth curves”。

表一、因变量多列型数据结构（n行记录、t列因变量）

ID	Y1	Y2	Y3	X	...
1	y11	y12	y13	x1	…
2	y21	y22	y23	x2	…
…	…	…	…	...	...
n	yn1	yn2	yn3	xn	…

在瘦长型结构中，因变量只占一列，但是每个个案占三列，因此因变量y1、y2和y3分布在这三行之中（见表二）。为了保留Y的观测时间点，新增加了一个变量Time，取值1、2、…、t。这种结构的正式学名叫做“multirecord format”（个案多行型），是HLM和其他多层分析软件所要求的数据格式。在这种数据结构中，你可以通过选择个人的ID来显示一个人的增长曲线，但也无法在同一图中显示多人的增长曲线。

表二、个案多行型数据结构（n x t行记录、1列因变量）

ID	Time	Y	X	…
1	1	y11	x1	…
1	2	y12	x1	…
1	3	y13	x1	…
2	1	y21	x2	…
2	2	y22	x2	…
2	3	y23	x2	…
…	…	…	…	…
n	1	yn1	xn	…
n	2	yn2	xn	…
n	3	yn3	xn	…

如要在同一图中显示多条增长曲线，需要将矮胖型或瘦长型数据转换成第三种结构，这在文献中还没有专门的名称，我姑且称之为individuals-as-variables format（“每人一列型”），如表三所示。这种结构更加“奇怪”，每一列是一个人的因变量或自变量，而每一行是一个时间点。本例t = 3，所以只有三行，比起矮胖型的n行来更加矮胖了。这种结构不适合做统计分析，但十分适合做各种图形，如可以做以Time为X-轴、单个或多个Y为Y-轴的增长曲线，也可以做以X为X-轴、Y为Y-轴的个人层面X-Y散点图。

表三、每人一列型数据结构（t行记录、n列因变量）

Time	ID1_Y	ID1_X	ID2_Y	ID2_X	…	IDn_Y	IDn_X
1	y11	x1	y21	x2	…	yn1	xn
2	y12	x1	y22	x2	…	yn2	xn
3	y13	x1	y23	x3	…	yn3	xn

好了，根据上述原理，你可以按需要而将数据在这三种结构之间互相转换。当然，如果你会使用SPSS的Syntax指令，确实可以用以下（或类似）的指令来“自动化”操作（注：指令中的大写字母是SPSS指令、小写字母是可以替代的变量名或文件名）。

*1. 假定你的数据是矮胖型结构，首先转换成瘦长数据.
VECTOR j=y1 to y3.
LOOP i=1 to 3.
COMPUTE y=j(i).
COMPUTE time=i.
XSAVE OUT 'r:\temp.sav'/KEEP id time y x.
END LOOP.
EXE.

*2. 随机抽取10个个案.
SAMPLE 10 FROM 100.  
EXE.
MATCH FILES FILE */KEEP id.    /*只保留被抽取的id.
AUTORECODE id/into newid.      /*对id重新排序.

*3. 与瘦长数据并行对接.
MATCH FILES TABLE */FILE 'r:\temp.sav'/BY id.
SELECT IF newid>0.     /*剔除没有newid的个案.
EXE.

*4. 从瘦长数据中逐个提取个案，分别保留到单独文件中.
DEFINE !newcase (!POS, !CMDEND).
!DO !i !IN (!1).
TEMP.
SELECT IF newid=!i.
SAVE OUT !QUOTE(!CONCAT('r:\newcase', !i, '.sav'))
  /KEEP time y x
  /rename (y=!concat('y', !i)/rename (x=!concat('x', !i).
!DOEND.
!ENDDEFINE.
!newcase 1 2 3 4 5 6 7 8 9 10.
EXE.

*5. 将10个单独文件平行对接起来，构成最后的“个案每列”结构.
MATCH FILES FILE 'r:\newcase1.sav'
  /FILE 'r:\newcase2.sav'
  /FILE 'r:\newcase3.sav'
  /FILE 'r:\newcase4.sav'
  /FILE 'r:\newcase5.sav'
  /FILE 'r:\newcase6.sav'
  /FILE 'r:\newcase7.sav'
  /FILE 'r:\newcase8.sav'
  /FILE 'r:\newcase9.sav'
  /FILE 'r:\newcase10.sav'.
EXE.

*6. 打印10个因变量对时间的散点图.
TSPLOT y1 y2 y3 y4 y5 y6 y7 y8 y9 y10/ID=time.

以下是步骤6制作的10条“个人增长曲线“图，估计就是你们要画的那种了。

如何处理自变量之间的相关关系？

JF @ 2010-03-15:

我有一个初级问题想了很久还是不清楚。假如我有一个因变量Y、两个自变量X和Z，如果做回归分析，只要将X和Z同时进入回归模型就可以了，不需理会X和Z的相关关系。但是如果用SEM，除了要分别连接X和Z对Y的路径，还要连接X和Z之间的相关关系。这是为什么呢？不是说在结构层面回归和SEM是一致的吗？

另外，在报告上述SEM结果时，是否需要描述和解释X和Z的相关关系？如果用回归分析，是否还需要另行计算X和Z的相关关系、然后再报告呢？

庄主 @ 2010-03-20：

你的问题确实简单、但绝非初级，因为其中涉及了回归分析与结构方程模型（SEM）的主要异同，值得讨论一下。首先，自变量与因变量之间的结构关系 (structural relationship among variables)，如自变量对因变量的直接影响、间接影响、总影响、交互影响、等等，在回归和SEM中都是同义的（但不一定是等值的，因为前者含有测量误差而后者不含测量误差，但这与本文无关，所以下面的讨论均假定所有变量都不含测量误差）。

但是，在处理自变量之间的相关关系时，两者所用的方法不同：回归是用隐含方法而SEM是用明示方法。在回归模型 Y = b₀ + b₁X + b₂Z中，对回归系数b₁和b₂的估算公式分别包含了X与Z的相关系数（记为r_XZ；同理，Y与X、Y与Z的相关系数分别记为r_YX和r_YZ）:

和

由于b₁和b₂是在Y与X或Z的简单相关系数中扣除了X与Z的相关程度（以及Y与另一自变量的相关程度），所以b₁和b₂又被叫做partial regression coefficients（偏回归系数）。可见，在回归分析中，自变量之间的相关关系是自动而且必须地被控制了的。这里的“被控制”是指用于消除自变量之间的相关关系的影响。

在SEM中，自变量之间的相关关系是需要明确设置的。如在使用矩阵语言的LISREL中，通过指令"FR PH (1, 2)”来估算r_XZ；而在使用图形语言的AMOS中，则是通过在X和Z之间画一条双箭头的曲线来估算r_XZ（见下图，注：图中的三个参数b₁、b₂和r_XZ是不需要的，这里只是为了说明它们与上述回归模型的对应关系）。

该SEM模型与上述回归模型是等价等值的。大家可以用一个含三个变量、N > 200 （SEM所需的最小样本量）的数据验证一下，两个模型的b₁、b₂、r_XZ、R-Square（= AMOS中的MSC）、Std error of the estimate（= SEM中e的Variance的平方根）应该都相等。然而，回归用的是OLS（最小二乘法）而SEM是用ML（最大似然法）来估算上述参数的。这两者之间的差别，除了对样本量的要求不同（ML估算只有在大样本条件下才可能接近OLS结果），还有许多深层的差别。这里只讲其中比较明显的一个差别：如上所示，r_XZ在回归中是自动被控制起来的，但在SEM中却需要人为设置。反过来说，如果需要的话，在SEM里也可以设置r_XZ = 0（在AMOS中也可以将X和Z之间的曲线删掉）或其它任意值（1.0，0.5，等等）。如此设置的模型，因为少估算了一个参数，所以会比原模型多出一个df（自由度），通过比较两个模型的拟合指数（Chi-squares）之差，就可以检验 r_XZ = 0（自变量之间为正交）或r_XZ = 1 （自变量之间没有discriminant validity）等假设。这些都是无法在回归分析中实现的。

回归模型与SEM模型之间更核心的区别在于前者是在变量层面检验自变量对因变量的解释程度、而后者则是在观察值的方差-协方差矩阵层面检验理论模型与实际数据之间的拟合程度。打个不完全恰当的比分，回归是西药，针对特定病症有强效，但不顾其它后果；而后者是中药，旨在整体和治本，但有时对特定病症并无速效。这种根本区别在本文讨论的自变量相关关系上也有一定影响，但这是一个大题目，需要很多基本概念和铺垫，否则难以讲清，所以不予展开，只是提醒大家，SEM的水很深，下水前要做足热身运动，而回归则是最好的热身运动。就如现在的中医学院都是先教西医原理、再进入中医的。

回到你最后那个问题：如何报告r_XZ？一般说来，自变量之间的相关关系（如r_XZ）是一种unanalyzed relationship（不作分析的关系）。这里的所谓“不作分析”指的不是统计分析、而是理论分析。如上所说，r_XZ在回归中是不直接计算的，但在SEM和用回归做路径分析中均需要统计分析的。但是，除非有特定研究目的（如上述检验自变量之间的discriminant validity）之外，大多数理论并不规定自变量之间关系的强度、方向（谁影响谁）、性质（正或负相关）等，所以实际研究中往往只是简单地估算它们之间的相关关系而不进一步深究其关系的性质、方向、性质等。在写报告时，如果用图形表示实证模型的话，可以在图上标出相关系数的估计值；如无图形，可在附录或注释中用文字或表格报告一下；但在正文中则一般不必提及。

清华SEM班邀请外校学生网上实时参与

课程名称：结构方程模型的原理与应用 Structural Equation Modeling: Principles and Applications

对象：清华大学新闻与传播学院硕博研究生及外校新闻传播院系本科1-3年级或硕士研究生1年级同学20人

时间：2010年5月15-24日

报名：2010年3月31日止

详见：http://www.tsjc.tsinghua.edu.cn/news.php?id=971

如何确定两个调节变量之间的主次关系？

SJ @ 2010-03-02:

祝老师您好！我是心理系的学生。在网上偶然逛到您的庄园，受益匪浅！非常感谢您的慷慨，跟大家分享您的所学所得。我最近在处理早前的一个数据，遇到困惑，不知道该怎么继续，想向您请教，先谢过。

我的数据涉及以下变量：一个自变量、一个因变量、四个假设的中介变量。另外人口统计学变量方面，考察了年龄（分成四个年龄组）和性别。我关注的是自变量如何通过中介变量影响因变量，以及这种影响是否存在年龄的发展差异。然而，我在做各个变量的相关时发现，性别跟好几个重要的变量都有显著的相关。因此我的困惑在于，我应该如何处理性别的问题。1.把性别作为调节变量，放到各个年龄组中来建立模型？2.还是每个年龄组都建立男生模型和女生模型？您觉得哪种方法更合适？具体又该怎么操作呢？

庄主 @ 2010-03-06:

谢谢与大家分享你的研究问题。这是一个相当复杂（其复杂程度应该远远超出你的预计，具体见下）的研究设计。我前天在我的课上介绍了你的问题，建议学生们来这里分享他们的看法。至今还没有人现身，也许是你的问题太难、也许是他们还没完成下周一交的作业。我先说一下解决方案的基本思路，希望他们能够接下去帮你解决方案的操作问题（同学们，这是你们给老师和学校挣面子的时候了）。

先整理一下你的问题所涉及的研究假设：

H1. 自变量X对因变量Y的直接影响（记为b_YX）。

H2. X通过中介变量M1-M4对Y的间接影响（分别记为b_Y(M1-X)、b_Y(M2-X)、b_y(M3-X)和b_Y(M4-X)）。

H3. 年龄A对直接影响b_YX的调节作用（即A与X对Y的交互效应，记为b_Y(X*A)）。

H4. 年龄A对间接影响b_Y(M1-X)等的调节作用（即A与X-M对Y的交互效应，分别记为b_Y((M1-X)*A)、b_Y((M2-X)*A)、       b_Y((M3-X)*A)和b_y((M4-X)*A)。注：因为X-M对Y是中介关系，所以A与它们的交互关系是一种被称为“moderated mediation“、即“被调节的中介关系”，相当复杂！）。

先在这里停一下。H1-H4可以用OLS回归来分析，但在SEM工具（如LISREL、AMOS等）中更方便。如用后者，需要把年龄当做组别，而将样本按年龄分成4组、通过比较组间的invariance来检验X对Y的直接和间接关系是否随着年龄的变化而不同（具体操作这里略过）。也就是说，moderated mediation关系，听起来很复杂，但在SEM中通过设置组间equality constraint的小技巧（或“小伎俩”？），很方便就能解决了。

好了，回到你最后的问题：如何检验性别S的影响？也就是检验以下假设：

H5. 性别S和年龄A对直接影响b_YX的调节作用（即S、A与X对Y的交互效应，记为b_Y(X*A*S)或b_Y(X*S*A)）。

H6. 性别S和年龄A对间接影响b_Y(M1-X)等的调节作用（即S、A与X-M对Y的交互效应，分别记为b_{Y((M1-X)*A*S)} 或      b_{Y((M1-X)*S*A)}等）。

你考虑了两种方案来检验H5和H6：一是将性别nested（嵌镶）到年龄中、二是将年龄嵌镶到性别中。表面上看，好像两者有根本区别，但实际上是一回事！性别和年龄是两个同等级别的调节变量，它们的联合影响是一种3rd-order interactions（三阶交互效应，也相当复杂），用公式来表述，如H5中的b_Y(X*A*S)或b_Y(X*S*A)，前者是年龄嵌镶在性别中、后者是性别嵌镶在年龄中，但无论谁嵌镶到谁中去，b_Y(X*A*S)和b_Y(X*S*A)两者是完全同价等值的。如果用SEM来检验，也无论谁嵌镶到谁中，你总需要将样本分拆成8个组（4个年龄组X2个性别组）。当然，在解读结果时，你可以而且需要根据自己的理论框架来确定A和S之间谁主谁仆的次序。

最后，要说一下检验如此复杂模型的成本问题。如上所说，如果用SEM，需要8个组；基于每个组涉及5个自变量（X、M1-M4），按每个自变量需要20个案来计，你至少需要每组100个案，总样本800个案。当然，你的年龄组分布可能不均匀，所以总样本很可能要1000以上。如果不用SEM而用回归，可以不分组，但是变成了一个非线性模型，涉及了24对二阶交互关系和12对三阶交互关系，即使总样本有1000个案，也只少不多。样本数少了、会有什么后果？你的中介效应、调节效应和被调节的中介效应都有可能不显著。其中的最薄弱环节是中介效应（H2）。所以，建议你先将H2分成H2a-H2d四个分假设，分别检验A和S对各分假设的调节作用（= 4 X  (4 X 3 /2) X 2 = 48个组间比较，如果你想不通为什么会有48个组间比较，请详细演算一下），以简化模型。

总结：中介效应、调节效应和被调节中介效应在理论上都是很吸引人的模型，但在实证上即昂贵又难操作，需要事先有充分的思想和技术准备。

如何理解SEM的八个参数矩阵与七种变量之间的对应关系？

s @ 2010-02-05:

 

曾看过你的帖子“LISREL的八个矩阵”，最近在学习用AMOS做SEM分析，不知两者有何关系？

 

庄主 @ 2010-02-15：

 

如我在上述帖子中说的，LISREL是用八个矩阵来设置SEM模型的。这些矩阵分别代表了SEM模型中七种变量的参数。在LISREL中，变量与参数之间的对应关系是比较明确、不易混淆的。如，大家知道，描述因子与其测量指标之间关系的参数叫做“因子负荷”，其中外生因子测量指标x的负荷矩阵是用Λ(x)来估算、内生因子测量指标y的负荷矩阵是用Λ(y)来估算的，两者不能放在一起（即外生因子无法与y相连而内生因子无法与x相连）。这种规定在大部分情况下是合理和必要的。（当然，少数情况下，研究者也许有特殊理由需要将x挂到内生因子上或y挂到外生因子上，就需要设定特殊的“All-y model”（全y模型）。这种额外步骤，虽然麻烦，但防止了初学者因不知情而乱点鸳鸯谱。）

 

AMOS是通过图像来设置模型的，用户不再需要与八个矩阵的希腊字母打交道，所设置的模型是“What you see is what you get”（WYSIWY），很容易上手、也避免了模型设置时的一些常见错误。但是，在这种“自由自在”的界面中，很容易犯一些LISRE里不会出现的错误。比如上面所说的，任意（或根据Modification Index的误导）将x挂到内生因子或将y挂到外生因子上去。这种模型或者无法identified、或者违反“误差项与自变量独立”的基本假定，因为AMOS以及其它SEM软件在估算模型的参数时，其实还是在背后使用上述矩阵。

 

为了帮助大家在用AMOS设置模型时避免设置不能或不该估算的参数，我在八大矩阵的基础上再做了一个表（见下），以显示八个参数矩阵与七种变量之间的关联与隔离：

 

 

表三的7列和7行分别代表了SEM的七个变量（包括外生因子ξ、内生因子η、η的误差ζ、外生因子的测量指标x、内生因子的测量指标y、x的误差δ、y的误差ε），它们在列里担任的是自变量的角色、而在行里担任的是因变量的角色。

 

两种变量相交的格里如果出现一个希腊字母，就说明它们之间存在一个参数矩阵（在下图中用黑色线条来表示）；而如果是个空格，就说明它们之间不能发生关系（在下图中用红线表示）。如第一列ξ与第一行ξ之间有个方差-协方差矩阵Φ（如下图中的φ₁₂）；第一列ξ与第二行η之间有个外生因子->内生因子的回归系数矩阵Γ（如下图中的γ₁₁和γ₂₂）；第二列η与第一行ξ之间是空白（即图中η₂到ξ₁的错误红线），因为内生变量不能影响外生变量（AMOS是可以让你画这条线的，但这在逻辑上是错的）；当然第二列η与第二列η之间是可以有一个内生因子->内生因子的回归系数矩阵Β（如图中的β₁₂和β₂₁）；等等。

 

表中还有三个记为“I”的矩阵，它们不在八个矩阵之内，而是三个对角线为1、其余部分为0的Identity矩阵，用来定义三种误差项变量（ζ，δ和ε）系数的数学工具，而AMOS在处理误差项变量系数时则是很“智能”的，会在相应处自动为它们标出取值为"1”的回归系数（见下图）。

 

LISREL的八个矩阵

(原版2007年5月19日，略有修改重发)

传说中的“八大军区联络图”终于出笼了：

上图看起来挺吓人的。别紧张，先定义一下。图中每个圆圈代表一个隐含因子、每个方块代表一个观测变量、每条直线或曲线代表一个参数（parameter，也叫系数）、跟在每条半封闭直线后面的是一个因子或变量的残差（error）。所谓“八大矩阵”，就是八种参数的集合。分别列在表一：

如表所示，其中前四个矩阵用于测量模型部分、后四个矩阵用于结构模型部分；每模型一部分又分别分为外生（即图一的左边）和内生（图一的右边）两边；每一模型部分的每一边，再分别分为关系参数和残差参数。即一个2 X 2 X 2的设计，十分严密。

上面的图和表中，都用到了希腊字母、而且大小写并用，实在是三难（难认、难读、难记，读音参见表二）。其实经典统计学中也用到一点希腊字母，其规则是：变量名用罗马字母（即英文）、参数用希腊字母（如回归系数叫BETA）；总体变量和参数用大写、样本变量和参数估计值用小写。LISREL大体上沿用了这些规则。然而，由于SEM中的变量有观测的和隐含的之分，LISREL的创始人Joreskog决定沿用罗马字母表示观测变量、但用希腊字母表示隐含因子。其用意可嘉、但结果使得参数和隐含因子分享同一套符号而产生了很多困扰。（如果该老友用禅经字母来表示隐含因子、那该多爽啊。）

八大矩阵是LISREL的核心思想，也是其与AMOS、EQS等其它软件的主要不同。其缺点如上所说，概念太多、名字难念、令人望而生畏。优点嘛，则见仁见智。我用了近20年，觉得其好处主要有两个：：一是便于区分外生因子（exogenous factors）与内生因子（endogenous factors）之间、隐含因子与观测变量之间、以及因子/变量的各种相关系数之间的差别；二是便于用户之间交流（包括写学术报告）时有一套确定而又简便的符号系统。

当然，是否值得仅仅为了这些好处而去重学一种外语（希腊语），则又是见仁见智了。我的看法，如果你用LISREL，那只能学；如果你用其它软件、但有志成为SEM的pro，那也要学一下（不然如果与主流沟通？）；如果你用其它软件而无意成为SEM方法专家，不学也罢，有所失必有所得。

如何识别回归分析中的压抑效应？

DHF @ 2010-01-25：

祝老师，您好，我是心理学专业学生，想向您请教一下，如何identify a variable as a suppressor variable in regression analysis? 我的数据中出现了类似于classical suppression的效应，但不清楚IV的regression weight提高多少才可以认为是suppression effect. 多谢！虎年顺利！

庄主 @ 2010-02-06:

Suppression effects（压抑效应）是回归分析中的一个重要而又复杂但却不常见的概念。你提到classical suppression（经典压抑），自然也知道此外还有net suppression（净压抑）和cooperative suppression（合作压抑）。相比之间，经典压抑最罕见（以下会谈到），但最容易确认。我用模拟方法做过经典压抑数据，但在实际研究中从来没有遇到过这种数据。你好像中了彩票，值得庆贺。如不怕泄露学术机密，不妨描述一下你的数据以及你认为可能的原因。我相信很多读者都会有兴趣了解。

考虑到大多数读者可能对压抑效应知之甚少，我先讲一些基本概念（估计你已经知道其中的大部分）。

为了便于叙述，我们只讨论含有两个自变量的回归模型，即 Y = B₁X1 + B₂X2。其中，B1和B2是标准化回归系数，所以没有常数项），另外记X1与Y的相关系数为r_y1、X2与Y的相关系数为r_y2、X1与X2的相关系数为r₁₂。 习惯上一般将X1看做主要的自变量而将X2看做是压抑变量。当然，X1和X2是对称的，完全可以将X1看做压抑变量的。

统计文献中有过不少压抑效应的定义，其基本思想基本一致，但具体公式上有所不同（所以结果也略有不同，但我不准备涉及那些技术细节）。就基本思想而言，压抑效应是根据r_y2 与 B2之间（或者r_y1 与 B1之间）的差别来确定的。具体说来，r_y2 可以取正值、负值和零值三种可能性，B2则有正值和负值两中可能（但B2不能为零，详见下文）。这样我们就要3 X 2 = 6种情况，分别属于经典压抑、净压抑和合作压抑：

1. r_y2 = 0而B2 > 0，叫做 positive classical suppression（正向经典压抑）；
2. r_y2 = 0而B2 < 0，叫做 negative classical suppression（反向经典压抑）；
3. r_y2 > 0而B2 > r_y2 ，叫做 positive cooperative suppression（正向合作压抑）；
4. r_y2 < 0而B2 < r_y2 ，叫做 negative cooperative suppression（反向合作压抑）；
5. r_y2 < 0而B2 > -r_y2，叫做 positive net suppression（正向净压抑）；
6. r_y2 > 0而B2 < -r_y2，叫做 negative net suppression（反向净压抑）。

上述六种情况，都包含|B2|>|r_y2|的条件，即一个自变量的回归系数之绝对值必须大于其与因变量的相关系数之绝对值。这是压抑效应的必要和充分条件。这里的“大于”、“等于”、“小于”、“差别”等，都是在统计显著性检验的含义上说的。如，在一个样本中，r_y2的值可以不是0、而是一个与0没有显著差别的数值（当然是一个很小的数）；而B2绝对值与r_y2绝对值之间的差别一定要达到统计显著水平（至少为p < 0.05）。当然，如何进行这种统计检验则不是一个容易的事，因为检验H0：|B2|=|r_y2|的零假设，需要有B2和r_y2的联合标准误差SE_B2,ry2，而无论相关分析和回归分析都无法计算SE_B2,ry2。

所幸的是这种困难对于经典压抑并不存在，因为根据定义，经典压抑的前提是r_y2 = 0，所以检验经典压抑只须证明当r_y2 = 0时，|B2| > 0（即上述情况1和2）。这大概就是你想知道的答案了。这么简单？是的。至今为止我看到的所有文献 都是这个意思。当然，|B2| > 0 仅仅表明B2有统计意义上的显著压抑效应，至于这种压抑效应是否具有实际或理论意义，则取决于B2的大小。这时，我们可以按判断回归系数大小的传统标准（如0.1为弱、0.3为中、0.5为强）来解读B2的压抑效应。

虽然我们无法对净压抑和合作压抑的零假设做正式的统计检验，但我们也可以援引上述rule of thumbs（惯例）来解释|B2|-|r_y2|的大小。（我在写这个帖子时，突然想到，也许这个问题可以在SEM中通过equality constraint的方法来解决。我一下子没想好，如有进展，会在这里报告。）

最后再补充一下：所谓“压抑效应”，是指上述回归模型因为引入了X2而将X1的方差中与Y无关之部分压抑或过滤掉了，从而改进或提高了该回归模型对Y的解释力。(The inclusion of X2 in the regression model suppresses or removes the part of variance in X1 that is unrelated to Y, which results in enhancement of the explanatory power of Y by the model.) 早年（也许是由于计算能力的局限），很多研究建立在相关分析基础之上，所以很有必要关注压抑效应的可能性。现在，多元回归分析是很多研究的起点。既然回归模型中已经同时考虑了X1和X2对Y的影响，那么X2的压抑效应已经被过滤了（当然也许还有X3、X4等等的压抑效应没有被过滤掉）。再加上压抑效应的数据不常见，所以现在很少人会检验压抑效应。但是，如果数据中真有压抑变量，其成因是很有价值的问题，弃之不顾太可惜了。同时，压抑效应的知识还可以帮助我们在研究设计阶段（即收集数据之前）将表面上与Y无关但与X1有关的X2包括在问卷或其它数据采集工具中。

如何比较一个自变量对三个因变量的影响大小？

ZYS @ 2010-01-23:

Dear Dr. Zhu,

I read your blog post on how to test the differences of two correlation coefficients posted on http://zjz06.spaces.live.com/blog/cns!3F49BBFB6C5A1D86!954.entry. Is it appropriate to use your method for two regression models based on one sample population?

My question is whether there is a appropriate way to test significant difference between regression coefficients of two different models from same sample population? For example in the below table, how would we statistically compare the difference between betas for political interest as predictors of DV in three conditions? This is a repeated measure experiment. the same group participants participated in three conditions in three months. In other words, the research question is whether the impact of political interest on opinion expression is moderated by condition... The reviewer wants a statistical test --but i didn't find a good way to test since they are not independent samples...

	Opinion expression in Condition 1	Opinion expression in Condition 2	Opinion expression in Condition 3
	ß	ß	ß
Education	.13*	-.07	-.06
Male	.10*	-.01	.05
Age	-.04	.28***	.31***
White	.04	.03	-.03
Political Interest	.33***	.10*	.08
R-square	.04	.09	.11
F	3.60**	7.48***	9.61***

Is there a better way this problem could be tackled?

庄主 @ 2010-01-24:

Your research question differs from the one in that post, where the issue is to compare the correlation coefficients between two independent variables (IVs) with the same dependent variable (DV) whereas your task is to compare the correlations between the same IV with three different DVs.

One approach you can consider is repeated measures regression in general linear modeling (GLM), in which you form a within-subjects (WS) factor to account for the three DVs, and then regress the WS factor on your IV and control variables.  To test the significance of the differences among the relevant regression coefficients, you use the procedure described in 如何检验两个回归系数的差别？.

Another approach, which I think simpler and easier to be understood, is to test a path model with  equality constraints in SEM (see the diagram below). Aside from your regular hypotheses, you fit a series of nested models to test the null hypothesis that β₁ = β₂ = β₃. For example, you compare the fully unconstrained model in which β₁, β₂, and β₃ are free to be estimated and the fully constrained model in which β₁, β₂, and β₃ are fixed to be the same.  The difference in the resulting Chi-squares between the two models, tested with Chi-square distribution with 2 degrees of freedom, tests the above null hypothesis.  In addition, you can test the fully constrained model with three partially constrained models, each with a pairwise constraint such as β₁ = β₂, β₁ = B₃, or β₂ = β₃, to entertain the possibility that not all three coefficients are exactly the same but some pair(s) of them may be. 

With the data in the table you provided, I guess that Condition 1 would be significantly different from Conditions 2 and 3 whereas the latter two might not. 

Good luck with your publication.  If it’s published, please come here to share your experience in getting published in journals.  Many readers of this blog would be very interested in learning from your experience.

如何解读回归与ANOVA的不同结果？

Anonymous @ 2010-01-22:

祝老师好！我是心理专业的学生，想请教一个具体的问题。对一个三类别变量作ANOVA结果显示类别1显著小于类别2和类别3，但将这三类转换为dummy variable，类别1为00，类别2为01，类别3为10，用同样的因变量来做回归时，结果是第一个dummy variable没有显著差异，而第二个dummy variable有显著差异，这是不是意味着类别2显著区别于类别1和类别3呢？如果是，为什么会出现这种结果呢？可能需要加上的是我在做回归时还引入了一些其它的变量，其中有一个会与类别变量有相关。

庄主 @ 2010-01-24:

将一个含3个类别的名目变量转换成两个dummy variables（分别记为D1和D2）后做回归分析，D1反映的是类别1和类别2的差别、D2反映的是类别1和类别3的差别。那么为什么类别1和类别2的差别在ANOVA中显著而在回归中不显示？因为你在回归中加入了其它自变量而成为多元分析而ANOVA是只有一个自变量的单元分析。其实，你可以将那些新加的自变量作为协方差 (covariates) 放入ANOVA的，这时就成了ANCOVA (Analysis of Covariates)，其结果应该与你做的回归分析完全一样。

你再问：D2为显著，是否说明了类别2显著区别于类别1和类别3呢？没有。D2只说明类别1和类别3的差别，与类别2无关。D1检验类别1与类别2的差别。如果希望知道类别2与类别3的差别，将类别2设为基准组（即类别2取00值，而类别1为10值），那么D2就是反映类别2与3的差别了。

如何检验交互效应的显著性？(更新版)

yxf @ 2009-12-29:

庄主您好：我是一名博士生，怀着非常忐忑的心情给您写这篇文章。我经常拜读您竹家庄上的文章，受益很深。您在2009年4月11日文章“如何绘制调节效应的图形？”，我能够看懂，但是用您的绘制调节变量的图形的方法于下面这篇文章得出的回归系数，和该文章得出的回归系数，为何不同？

这是发表于《管理世界》2009年第一期的一篇文章（下面复制了它的两个图和一段文字）。

首先，根据您的绘制调节变量图形的方法，

Y = 0.405X + 0.360Z - 0.186XZ + 常数 =（0.405 - 0.186Z）x + 0.360Z+常数

（1）低中国人传统性，取Z为均值减一个标准差，为-0.647，此时Y = [0.405 - 0.186 × (-0.647)]X + 0.360 × (-0.647) + 常数 = 0.525X+常数

（2）高中国人传统性，取Z为均值加一个标准差，为0.647，此时Y = [0.405 - 0.186 × (+0.647)]X + 0.360 × (+0.647) + 常数 = 0.525X + 常数 = -0.285X + 常数

但是，为什么这篇文章得出的结果不同呢？

（1）低中国人传统性，Y = 0.503X + 常数 （p＜0.01）

（2）高中国人传统性，Y = 0.018X + 常数 （p＞0.01）

这篇文章的结果正确吗，它是如何计算出来的，特别是它的p值是如何计算出来的？是不是我没有正确领会您的“如何绘制调节效应的图形？”的内涵？

（庄主注：yxf的信中附有原文的部分页面，因涉及版权，这里删去。有兴趣者请参阅：汪林、储小平、倪婧：“领导—部属交换、内部人身份认知与组织公民行为”,《管理世界》2009年第1期，97-108页。)

庄主 @ 2009-12-30：

你提了两个问题。一是如何计算“低传统”组和“高传统”组各自的回归斜率；二是如何检验这些斜率的统计显著水平？以下分别简答之。

一、如何计算分组回归斜率（也叫“简单斜率”）？我在多个前贴（包括你提到的“如何绘制调节效应的图形”一文）中已介绍过，简单斜率是根据总样本回归模型

Y = b0 + b1X + b2Z + b3XZ                 (1)

而计算出来的。即先选定若干个Z的值（如本例中小于和大于“传统性”均值的一个标准差，分别记为Z1和Z2），然后代入公式1，就有

Y = b0 + b1X + b2Z1 + b3XZ1 = (b0 + b2Z1) + (b1 + b3Z1)X            (2)

和

Y = b0 + b1X + b2Z2 + b3XZ2 = (b0 + b2Z2) + (b1 + b3Z2)X             (3)

其中b1+b3Z1是低传统组的简单斜率、b1+b3Z2是高传统组的简单斜率。这种方法，与论文作者所参照的Aiken and West (1991)的方法是完全一样的。

至于具体计算，只是做简单的加减乘，没有特别深奥的地方。当然，先要弄清Z1和Z2是原始数据还是取中值 (centered score)。在本例中，前者为3.52±0.647而后者为±0.647（因为取中值的均值为0）。你是用后者来计算的，你的结果中低组的斜率是对的（0.525），但高组的斜率错了，应该也是正数（0.285）而不是负数（-0.285）。我估计你算对但写错了。

作者为什么算出来分别是0.503和0.018？我看了原文，他们没有交代用的是原始数据还是取中值。如果用的是原始数据，结果应该分别是-0.129和-0.370，与其上下文不合。估计他们用的是取中值，但手算时出错了。你不妨直接写信问他们一下？

二、如果检验简单斜率的显著性？我在有关前贴中也应该讲过，但一下子查不出来，所以再讲一下。我们知道，一个回归方程的斜率（如b1），可以用t = b1/se_b1 来检验。同样，简单斜率b1+b3Z的显著性也是用一个类似的 t-检验来完成的（注意，要将这里的b1+b3Z当做一个常数来看），即

                          （4）

其中的分母就是简单斜率的标准误差，SPSS或其它统计软件不会直接报告这个参数，但可以根据以下公式

                    （5）

手工算出，其中的se²_b1和se²_b3分别是b1和b3的方差(variance)、cov_b13是b1和b3的协方差(covariance)（注意：这里提到的是b1和b3的方程-协方差而不是X和Z的方差-协方差），在SPSS中在Statistics的选项中选择“BCC”可以获得这些参数，而这里的Z则用上述的Z1或Z2值来代入。

算出公式4的t-值后，就可以查表得出其相对应的p-值了。估计原文作者就是这么做的。当然，他们如果报告一下两个t-值和对应的两个p-值各为多少，就更令人信服了。

yxf @ 2010-01-07

庄主，您好：非常感谢您的回复。我非常仔细地学习了您的“如何检验交互效应的显著性？”，感觉帮助非常大。在您的回复中，“二、如果检验简单斜率的显著性？”有一段话

“简单斜率b1+b3Z的显著性也是用一个类似的 t-检验来完成的（注意，要将这里的b1+b3Z当做一个常数来看），即公式4（省略），其中的分母就是简单斜率的标准误差，SPSS或其它统计软件不会直接报告这个参数，但可以根据以下公式5（省略）手工算出，其中的se²_b1和se²_b3分别是b1和b3的方差(variance)、cov_b13是b1和b3的协方差(covariance)（注意：这里提到的是b1和b3的方程-协方差而不是X和Z的方差-协方差），在SPSS中在Statistics的选项中选择“BCC”可以获得这些参数，而这里的Z则用上述的Z1或Z2值来代入。”

这里，se²_b1、se²_b3、cov_b13在SPSS中的计算方法我不太确定如何操作，因为不知道BCC是如何操作的？我找到两种方法，您认为哪一种方法算出的协方差是适合本文这里使用的，因为这两种方法算出的协方差不一致：

1. Analyze—>Regression—>Linear—>Statistics—>Regression Coefficients中 "Covariance Matrix” 打钩，然后算出协方差矩阵；
2. Analyze—>Correlate—>Biraviate—>Options中 "Cross-Product Deviations and Covariances” 打钩，然后算出协方差矩阵。

您认为哪一种方法是正确的，还是都不正确？正确的方法应该如何操作？

另外，“cov_b13是b1和b3的方差-协方差而不是X和Z的方程-协方差”，这两个协方差有何区别？

万分感谢！

庄主 @ 2010-01-16：

用方法1而不是方法2。如我原文中所说，前者是回归系数(b1, b2, b3）之间的方差-协方差、而后者是自变量（X, Z）之间的方差-协方差，是风马牛不相及的完全两回事。

大家应该对后者很熟悉，即使不那么熟悉、但在学习初级统计的相关系数部分时、多半也看到过相关系数与协方差之间的转换关系（Cov_xz = r_xzsd_xsd_z，即X和Z的相关关系r_xz乘上X和Z各自的标准差sd_x和sd_z就是X和Z的协方差Cov_xz）。很多学生对我说，他们的老师没有讲过这个公式。我的回答一般是“这还需要讲吗？”。比较一下相关系数的公式和协方差的公式，前者不就是少了sd_x和sd_z吗？甚至记不得公式，但一定知道相关系数是标准化的协方差、而协方差是非标准化的相关系数吧？将一个标准化的指标乘上其标准差不就是其非标准化的指标了吗？反之，将一个非标准化指标除以去标准差不就是标准化了吗？当然，如果只是通过老师的PPT讲义和点击SPSS菜单而学习统计的话（很可惜，现在的社会科学学生中大概99%是这么过来的），这些ABC原理都好像很陌生。青年朋友们：不要做PPT和SPSS的奴隶，多看书、并且经常手工演算各种公式吧。

那么前者呢？很可能你们老师们没有讲过。其实我的老师们（当中不乏顶尖学者）也都没有讲到，因为回归系数的协方差一般用不到。曾有一位美国名校名导师培养出来的博士朋友问我，b1和b3是两个常数、它们之间怎么可能有相关系数呢？是的，回归系数是常数，但任何统计量（常数）都有一个抽样分布（即假定从同一总体中抽取无数个相同大小的样本，做同一回归而得到的无数个回归系数就构成了一个服从t的抽样分布），在这个抽样分布中的每个回归系数都是一个变量（而不是常数），所以各自都有自己的方差、而相互之间就有相关系数或协方差。