如何检验两个模型拟合度的差别？

Anonymous @ 2010-09-01:

祝老师您好！我看了您对“为何不同模型的路径系数和拟合度相同”一文的回复，有一处不明白。想向您请教。即，当两个模型对同一组数据的拟合都可以接受时，如何检验这两个模型的拟合度之间有没有显著差异呢？

庄主 @ 2010-09-02:

首先要分清这两个模型之间是否具有从属关系。如果是的，可以用常规的模型比较方法来检验；否则需要用非参数的统计量。下面分别说一下。

主从关系模型之比较

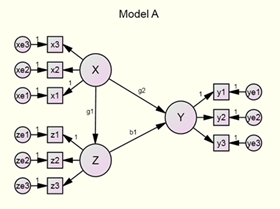
什么是模型之间的主从关系 (hierarchically nested)？如果两个模型（A和B）具有相同的变量（包括隐含因子和观测指标）、而其中模型B是在模型A的基础上减去若干参数，这两个模型就被认为是有主从关系。按参数的个数来看，模型A是主（full model）、模型B是从（reduced model）。请看以下例子：

上图中，A和B在measurement model（测量模型层面）上完全相同；但在structural model（结构模型层面）上则不同：在A中因子X对因子Y有直接影响（记为g2），而在B中X对Y没有直接影响（也即g2=0）。这两个模型之间就是具有上述的主从关系，所以可以直接用常规的模型比较方法对两者之间的差别进行显著性检验。

所谓“常规的模型比较方法”，是指计算两个具有主从关系的模型的卡方值（分别记为χ_Asup>2和χ_Bsup>2）之差（记为Δχ²），然后根据两个模型的自由度（分别记为df_A和dfχ_B）之差（Δdf），从卡方分布表中查出该Δχ²），所对应的显著水平（p-level）。

以上图中的模型A和B为例。假定A的χ_A² = 150.0而B的χ_A² = 145.0，Δχ² = 150.0 - 145.0 = 5.0，而df_A = 22（这不是假定而是实际的，因为该数据有45个已知值、23个参数；大家可参照前贴如何计算SEM中的自由度？来计算本例各模型的自由度）、df_B = 23（很显然，因为B少用了一个参数、因此多一个自由度）、Δdf = 1。根据卡方分布表（可参考以下http://www.fourmilab.ch/rpkp/experiments/analysis/chiCalc.html），如果df = 1而χ² = 5时，其对应的p-level = 0.0253。那么，我们的结论是什么呢？即，A和B之间是否有显著差别呢？或者，在A和B之间我们应该选择哪个呢？请大家自己得出结论。如果有疑问，请继续提出。

非主从关系模型之比较

如果两个具有同样变量的模型之间没有上述的hierarchical nested关系，就无法直接比较了。上图中，A和C也是有主从关系的，但B和C却不具备主从关系，尽管两者都是A的从属。两个非主从关系的模型之间的比较，一般是用Akaike Information Criterion (AIC)或类似的非参数统计量（non-parametric statistics）如Bozdogan's Consistent AIC (CAIC)或Browne-Cudeck Criterion (BCC)。所谓“非参数统计量”是指该统计量的概率分布（也就是说其显著性水平）是个未知数。所以比较两个非主从关系的模型之间AIC（或其它）的差别，我们只能知道其中那个模型对数据的拟合更好一些、但不能确定这种差别在总体里是否存在。

以上图的B和C为例，假定AIC_B = 120和AIC_C = 135，我们可以知道B对数据的拟合更好（因为AIC及其它类似统计量都是越小越好），但是我们无法得知ΔAIC = 15的p-level是什么。因此，非主从关系的模型之间的比较，只是非正式的研究。

如果一定要检验两个非主从关系模型之间差别的显著性，那就需要找到一个B的替身（且称为B’)，其即同时为B和C的主模型、但又与B没有显著差别。在本例中，A是B和C的主模型、但是与B有显著差别，所以不能承担B的替身。如果能找到B’，那么B’与C是主从关系，就可以按上述的常规模型比较方法来检验B’与C的差别了。