JF @ 2010-03-15:
我有一个初级问题想了很久还是不清楚。假如我有一个因变量Y、两个自变量X和Z,如果做回归分析,只要将X和Z同时进入回归模型就可以了,不需理会X和Z的相关关系。但是如果用SEM,除了要分别连接X和Z对Y的路径,还要连接X和Z之间的相关关系。这是为什么呢?不是说在结构层面回归和SEM是一致的吗?
另外,在报告上述SEM结果时,是否需要描述和解释X和Z的相关关系?如果用回归分析,是否还需要另行计算X和Z的相关关系、然后再报告呢?
庄主 @ 2010-03-20:
你的问题确实简单、但绝非初级,因为其中涉及了回归分析与结构方程模型(SEM)的主要异同,值得讨论一下。首先,自变量与因变量之间的结构关系 (structural relationship among variables),如自变量对因变量的直接影响、间接影响、总影响、交互影响、等等,在回归和SEM中都是同义的(但不一定是等值的,因为前者含有测量误差而后者不含测量误差,但这与本文无关,所以下面的讨论均假定所有变量都不含测量误差)。
但是,在处理自变量之间的相关关系时,两者所用的方法不同:回归是用隐含方法而SEM是用明示方法。在回归模型 Y = b0 + b1X + b2Z中,对回归系数b1和b2的估算公式分别包含了X与Z的相关系数(记为rXZ;同理,Y与X、Y与Z的相关系数分别记为rYX和rYZ):
和
由于b1和b2是在Y与X或Z的简单相关系数中扣除了X与Z的相关程度(以及Y与另一自变量的相关程度),所以b1和b2又被叫做partial regression coefficients(偏回归系数)。可见,在回归分析中,自变量之间的相关关系是自动而且必须地被控制了的。这里的“被控制”是指用于消除自变量之间的相关关系的影响。
在SEM中,自变量之间的相关关系是需要明确设置的。如在使用矩阵语言的LISREL中,通过指令"FR PH (1, 2)”来估算rXZ;而在使用图形语言的AMOS中,则是通过在X和Z之间画一条双箭头的曲线来估算rXZ(见下图,注:图中的三个参数b1、b2和rXZ是不需要的,这里只是为了说明它们与上述回归模型的对应关系)。
该SEM模型与上述回归模型是等价等值的。大家可以用一个含三个变量、N > 200 (SEM所需的最小样本量)的数据验证一下,两个模型的b1、b2、rXZ、R-Square(= AMOS中的MSC)、Std error of the estimate(= SEM中e的Variance的平方根)应该都相等。然而,回归用的是OLS(最小二乘法)而SEM是用ML(最大似然法)来估算上述参数的。这两者之间的差别,除了对样本量的要求不同(ML估算只有在大样本条件下才可能接近OLS结果),还有许多深层的差别。这里只讲其中比较明显的一个差别:如上所示,rXZ在回归中是自动被控制起来的,但在SEM中却需要人为设置。反过来说,如果需要的话,在SEM里也可以设置rXZ = 0(在AMOS中也可以将X和Z之间的曲线删掉)或其它任意值(1.0,0.5,等等)。如此设置的模型,因为少估算了一个参数,所以会比原模型多出一个df(自由度),通过比较两个模型的拟合指数(Chi-squares)之差,就可以检验 rXZ = 0(自变量之间为正交)或rXZ = 1 (自变量之间没有discriminant validity)等假设。这些都是无法在回归分析中实现的。
回归模型与SEM模型之间更核心的区别在于前者是在变量层面检验自变量对因变量的解释程度、而后者则是在观察值的方差-协方差矩阵层面检验理论模型与实际数据之间的拟合程度。打个不完全恰当的比分,回归是西药,针对特定病症有强效,但不顾其它后果;而后者是中药,旨在整体和治本,但有时对特定病症并无速效。这种根本区别在本文讨论的自变量相关关系上也有一定影响,但这是一个大题目,需要很多基本概念和铺垫,否则难以讲清,所以不予展开,只是提醒大家,SEM的水很深,下水前要做足热身运动,而回归则是最好的热身运动。就如现在的中医学院都是先教西医原理、再进入中医的。
回到你最后那个问题:如何报告rXZ?一般说来,自变量之间的相关关系(如rXZ)是一种unanalyzed relationship(不作分析的关系)。这里的所谓“不作分析”指的不是统计分析、而是理论分析。如上所说,rXZ在回归中是不直接计算的,但在SEM和用回归做路径分析中均需要统计分析的。但是,除非有特定研究目的(如上述检验自变量之间的discriminant validity)之外,大多数理论并不规定自变量之间关系的强度、方向(谁影响谁)、性质(正或负相关)等,所以实际研究中往往只是简单地估算它们之间的相关关系而不进一步深究其关系的性质、方向、性质等。在写报告时,如果用图形表示实证模型的话,可以在图上标出相关系数的估计值;如无图形,可在附录或注释中用文字或表格报告一下;但在正文中则一般不必提及。

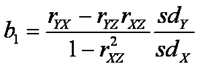
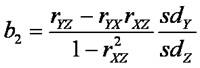




1 comment:
Thanks for your sharing! It really helped!
Post a Comment