如何处理SEM模型中的“坏”因子？

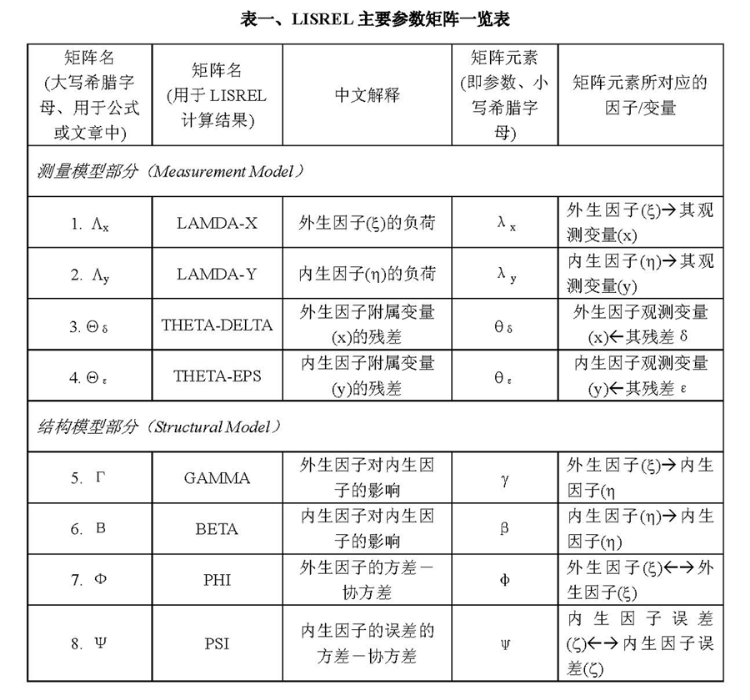
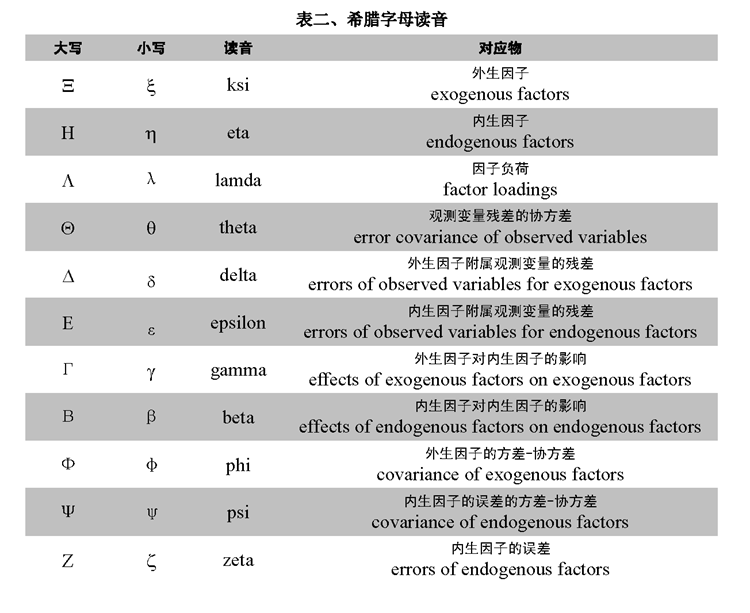
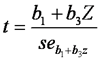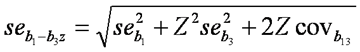SJ @ 2010-05-17:

我是X大学心理系的学生，目前在美国Y校访问。最近在处理数据时遇到问题不知该如何解决，之前在您的网页上冒昧向您请教过，非常感谢您当时的回复。我后来找了一些相关的文献看，知道了多组比较的大概步骤，但在统计中又遇到了新的问题，所以再次向您请教。谢谢您关注我的邮件！

我探讨的是暴力游戏对青少年攻击性影响的性别与年龄差异。研究变量包括：

• 自变量：玩暴力游戏的程度(VVG -- 庄主注，下同)
• 因变量：身体攻击(Physical Aggression)
• 中介变量：信念(Belief about Aggression)、期望(Hostile Expectation)、移情(Empathy)
• 调节变量：性别、年龄

因此我把全部被试（795人）按年级和性别分成六个组，每组100多人，想比较不同性别、不同年龄孩子模型的路径差异（庄主注：这应该是一个moderated mediation模型，对此有兴趣的读者请仔细理解本案例的模型设置及有关讨论）。

比较结构模型前，为了确定测量等同(measurement invariance -- 庄主注)，我分别对信念、移情和身体攻击这三个潜变量进行了单组和多组的CFA。以因素负荷相等(factor loadings invariant -- 庄主注)为标准，最后确定了5项目的信念、5项目的身体攻击及12项目的移情测量，能够满足跨组测量等同。信念和身体攻击是完全等同，两个移情项目虽不等同，但考虑到12题中只有两题不等同，所以认为部分等同也能允许进入结构模型的比较。

上面我所提及的CFA是分别针对每一个变量（庄主注：应该是factor吧？）进行的。但当我把所有变量（庄主注：也是factors吧？）都整合到一个模型后发现，六组都不能很好地拟合总模型。我看了修正指数（modification index或MI -- 庄主注），发现问题主要出在移情这个变量上。在前面的测量等同阶段，我删掉了16个移情项目，保留了12个项目，这12个项目分属5个因子。在结构模型中，我把这个5个因子作为移情的指标（庄主注：Empathy成了一个second-order factor？），但发现指标间及指标与其他变量还存在复杂的关系，这导致了模型不能较好拟合。

我又尝试了很多次，尝试找到一个移情的测量模型（measurement model -- 庄主注），无论是单个变量的单组及多组CFA，还是放到总模型中时，都能拟合六组数据，但徒劳无功。

如果把所有变量都当成显变量，那模型都能拟合得很好。但我能这样做吗？如果把所有变量当成显变量来处理的话，那前面的测量等同检验是否还有必要？

我实在不知道该如何考虑和继续，所以冒昧请教，请您给予我指导，非常感谢！

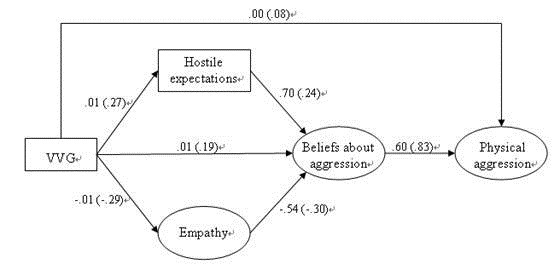
附件的图是我在确定了各组的测量等同后，用总数据做的模型。我担心我说得不清楚，可能看看模型会有帮助。再次感谢！

X²(114) = 411.1, p < .001, RMSEA = .06, NNFI = .90, CFI = .91

Note: Unstandardized coefficients are provided first, with standardized coefficients in parentheses. All paths are significant.

SJ @ 2010-05-21:

在等待您的回复之余，我这几天仍然在尝试寻找拟合潜变量的总模型，但可恨NNFI仍徘徊在0.8几（如果拟合很差我也就放弃了）。我发现问题在于移情量表。因为当我把三个潜变量当中的移情视为显变量，保留攻击与信念作为潜变量时，模型的拟合是可以的。移情的四个子量表之间有复杂的关系，而这不是我这个研究想关注的问题。我该如何处理呢？

庄主 @ 2010-06-13:

正如我在你上面叙述中加注所说，你想研究的是一个moderated mediation (“被调节的中介效应”？) 模型。虽然这种模型有点复杂，但是你遇到的三个问题（见下），却是在其它各种模型中也经常会出现。

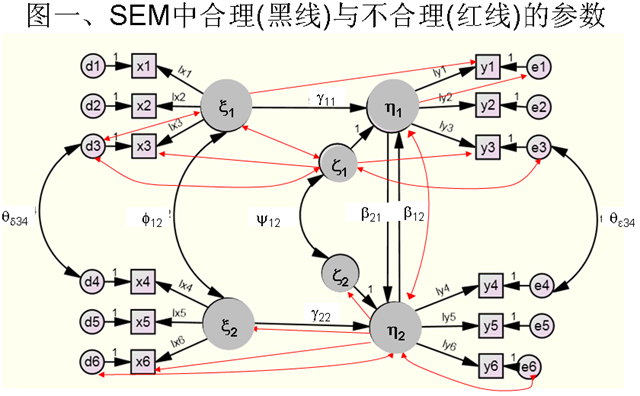
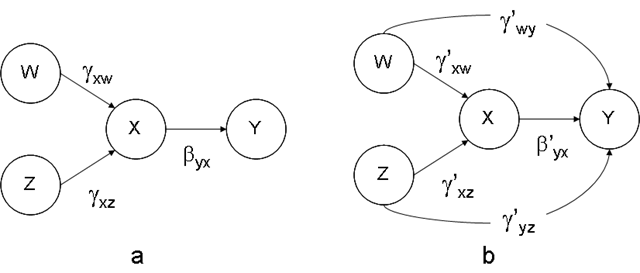
一、为何你对三个中介变量分别做CFA时各自都拟合得很好，但当将三个因子合在一起做CFA时却拟合不好？这很常见。一般而言，单个因子CFA（即只有一个因子的模型）非但没有意义、而且富有误导性。实际研究中，最简单的模型至少也有两个因子。而拟合任何一个多因子模型，则不但需要每个因子内部的测量指标之间高度相关，而且需要各因子之间的测量指标基本独立（见下图a）。而如果数据是下图b那样，则会出现单因子模型拟合很好而多因子模型拟合不好的现象。在本例中，如果分别拟合X1-X3和Y1-Y3，会得到两个很完美的模型，但那是假象，X1-X3和Y1-Y3实际上应该同时属于一个因子。

二、为何总样本的拟合度要比六个分样本的拟合度好？你没有这么说，而是我从你提供的总样本模型拟合度（应该是勉强可以接受）和对分样本结果的叙述（如“六组都不能很好地拟合总模型”和“NNFI仍徘徊在0.8”等）中推出。这应该与你的分组样本过小有关。如你所说，每个分样本100余人，而每个模型含30来个测量指标（（= 22个中介变量指标 + ？个自变量指标 + ？个因变量指标）。计算样本量是否足够的一种快捷方法（不一定精确但大体上可靠）是样本量除以测量指标数。文献中最宽松的说法是应该大于10（我倾向于更大一些）。而你这里只有4-5之间。样本小的一个直接结果是指标之间的相关程度不稳定（可以更高或更低）。回到上图，总样本容易接近a，而分样本则难。这里不怕因子内部相关程度变低，而是拍因子之间相关程度变高。

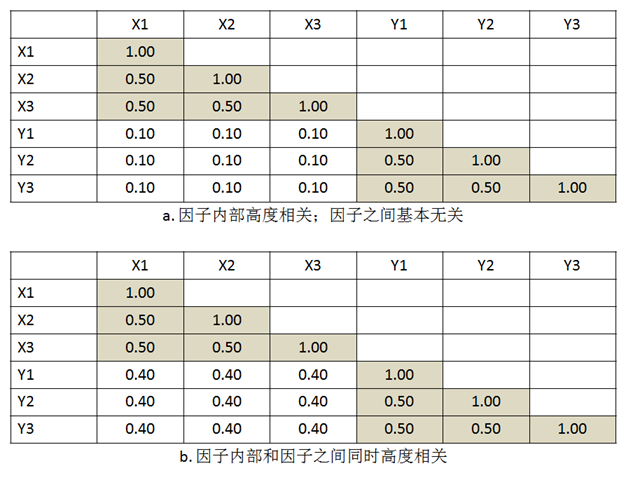
改进的方法包括：增加样本（你大概做不到）；减少分组（如两个年龄组 X 两个性别组 = 4）；减小测量指标数（尤其是“移情”用了12个指标，有必要那么多吗？）等。

三、“移情”是个“坏”因子，是否可以将其12个测量指标直接进入模型（即你说的“显变量”）？如果为了提高拟合度，当然可以这么做。但是，这在理论和统计上都是下策。首先，显变量都是含测量误差的；其次，一个含12个显变量作为中介变量的模型是无比复杂；再次，部分（或很多）显变量之间会有共线性问题；等等。所以，你得到了模型拟合度的改进，但失去了更多。

我并不了解你的“移情”量表之来历，估计是个已被前人验证的成熟（？）工具。如此，为何在本案中成为“搞坏了一锅汤的老鼠屎”呢？也许是问卷翻译的问题？或是被测对象的不同（文献中的移情是用于儿童的吗）？还是加在其它问题之后（？）产生的副作用？等等。可能有很多种原因。你说移情不是你本研究想关注的问题。但是，如果该因子的测量模型太有问题，那么，你只能在整体删去这个因子和显变量处理之间做出痛苦的选择。如果是我，会选择前者。

为何一个自变量在总样本和分样本中的显著性不同？

Anonymous @ 2010-06-02:

老师：您好。我在做回归分析的时候遇到一个问题，想向您请教。假设我用一些自变量解释因变量y

y=a0+a1x1+a2x2+...+anxn     (模型1)

最后得到的结果是x1(如非农收入比重)，x2(如政府补助)与y1显著相关(p<0.01)。我的指导老师希望我对样本进行分组，分为参与非农产业与未参与非常产业，然后对两个子样本分别进行回归分析。他想考察参与非农产业与不参与非农产业的情况下，x2对y的解释力是否有差异。得到两个模型：

参与非农产业的样本（样本2）：y*=a0*+a2*x2*+...+an*xn* （模型2）

不参与的样本（样本3）：y‘=a0’+a2‘x2’+...+an‘xn’ （模型3）

结果模型2里，x2与y之间显著相关，模型3里二者并不相关。我的指导老师就说这是因为，x2与y之间之所以显著，就是因为在样本2里二者有显著相关关系。对于不参与非农产业的样本，x2与y之间并无关系。因为我对统计知识一无所知，所以上来向老师求助。我的指导老师的说法对吗？出现这种结果还可能是什么原因？或者怎样理解这种现象？

期待您的回复，谢谢

庄主 @ 2010-06-05：

虽然你描述了很详细，但我还不敢肯定完全清楚你的数据（如Y是什么？）和以及你指导老师的意思（他的话“X2与Y之间之所以显著是因为两者有显著相关关系”好像是同义词重复？）。

我猜，你的核心问题是为什么X2在总样本和分样本1中对Y有显著影响，但在分样本2中没有显著影响？假定你是根据X1而将总样本一分为二的（因为X1没有出现在模型2或3中），那么X2只在分样本1中显著的原因有二：

一、X1与X2对Y有交互影响（interaction）。简单说来，X2对Y的影响不是一个常数，而是随着X1的值而变化，如当X1 > 0 (是吗？)时，X2对Y有显著影响；而当X1 = 0（是吗？），X2对Y并无显著影响。至于为什么会这样，则是需要用你们的专业知识来解释了。

二、由两个分样本的大小不同而造成。我们知道，相关系数或回归系数的显著性与样本大小直接有关。如果两个样本的大小不同，即使两者的相关系数或回归系数相同，其中大样本的系数可能显著而小样本的系数则可能不显著。这是一种方法上的artifact（即人为假象）。你需要检查一下两个分样本的大小是否相同。

事实上，如我在前贴（如“分样本比总样本的回归分析更准确吗？”）中指出，检查X1和X2的交互影响，不应该将样本按X1的值分成两个分样本来比较a2，而是应该在总样本（即你的模型1）中加入X1和X2的交互项（即X1和X2的乘积），用你的模型术语来表示，即为 Y = a0 + a1X1 + a2X2 + a3X1X2 + ... + anXn。其中a3的显著性直接检验了a2是否随着X1的变化而显著变化，并避免了因为将总样本分成分样本而造成的人为不显著假象。

如何比较自变量与中介变量的解释力？

YF @ 2010-04-19：

庄主，非常感谢您对学生的慷慨指导，我想向您请教一个新问题。《管理世界》上有篇文章（见以下出处），是研究中介效应的，其自变量是家长式领导方式，应变量是团队绩效，团队冲突管理方式。作者按照Baron & Kenny（1986）检验中介变量的方法，分析结果用表2表示。

我的问题和该作者文章没有关系，是以该文章为例：（1）如果比较中介变量和自变量对应变量的解释力是否有意义？（2）如果有意义，是否根据下表2结果可以比较中介变量和自变量对应变量的解释力？如果可以根据下表2结果比较，那么看哪两个数据？例如：如果比较仁慈领导和合作型团队冲突解决方式对团队绩效的解释力，是根据0.726**（model 3）〉0.513**（model 2），还是根据0.662**（model 4）〉0.126（model 4），认为仁慈领导对团队绩效的解释力大于合作型团队冲突解决方式对团队绩效的解释力。

文献出处：张新安, 何惠, 顾锋. 家长式领导行为对团队绩效的影响：团队冲突管理方式的中介作用. 管理世界, 2009, 3: 121-133.

庄主 @ 2010-04-21：

问题1：比较中介变量与自变量之间对因变量的解释力之差别，是否有意义？有，但这只是检验中介效应的规定动作之一。强度版的中介效应要求自变量（X）对因变量（Y）的直接影响（Byx）= 0 而其通过中介变量（W）的间接影响（RwxByw) > 0；而弱度版的中介效应则要求Byx < RwxByw。也就是说，Byx < Byw是中介效应的必要条件（因为Rwx小于1.0）。所以两者的差别是不喻而言的。如果Byx大于或等于Byw，那就没有必要再谈中介效应了。

问题2：如果比较Byx与Byw的大小，应该看模型4。你的困惑来源于作者不合适、也无必要用了四步的hierarchical回归（“分批进入回归”，参见我数贴中对在类似场合下使用这种方法的批评），模型2（自变量模型）和模型3（中介变量模型）的系数是不能直接比较的，因为模型2中的Byx是在Byw缺席情况下估算的，其中含有通过Byw的间接影响，所以是夸大了的；同样，模型3中的Byw的影响也因为由于Byx的缺席而被夸大了。只有两者同时出席的模型4才是直接比较的地方。

当然，模型2和模型3也有其用此，就是通过计算模型4的R平方 - 模型2的R平方（= 0.505 – 0.307 = 0.198）来得知两个中介变量（合作型和竞争型）对因变量的联合解释力，并通过计算模型4的R平方 - 模型3的R平方（= 0.505 – 0.478 = 0.027）来得知三个自变量（权威、仁慈、德行）对因变量的联合解释力。而表中模型2和模型3的ΔR平方则是没有什么意义的。由于很多读者对此有困惑，我再重复一下这种“nested testing”（嵌镶式检验）与上述“分批进入回归”的区别：

假定模型为Y = b0 + b1X1 + b2X2 + b3X3，分批进入回归的做法是估计三个模型，分别为Y = b0 + b1X1, Y = b0 + b1 + X2, Y = b0 + b1X1 + b2X2 + b3X3，然后认为：模型1的R平方代表X1对Y的解释力、模型2的R平方与模型1的R平方的差别为X2对Y的解释力、模型3的R平方与模型2的R平方的差别为X3对Y的解释力。其问题是模型1的R平方中包含了X2和X3的贡献、模型2的R平方中包含了X3的贡献。

嵌镶式检验是估计四个模型，分别为1：Y = b0 + b1X1 + b2X2 + b3X3（全模型），2：Y = b0 + b2X2 + b3X3（X1缺席模型），3：Y = b0 + b1X1 + b3X3（X2缺席模型），4：Y = b0 + b1X1 + b2X2（X3缺席模型），然后认为：模型1与2的R平方之差为X1对Y的独立解释力、模型1与3的R平方之差为X2对Y的独立解释力、模型1与3的R平方之差为X3对Y的独立解释力。这里的最后一步与分批进入回归的最后一步相同、但其它比较有数量和质量上的区别。注意，嵌镶式检验的三个R平方差其实就是模型1中X1、X2和X3的semipartial correlation，在SPSS中叫做“part correlation”，可以只估算模型1而得知，不需再分别运行模型2-4的。对初学者来说，分别操作一下有助于从理念上认识上面讨论的各种问题的逻辑。

如何绘制个人增长曲线图？

Z @ 2010-04-15:

我们有一3个wave的panel样本，用GLM Repeated Measures分析数据，并从中画出三个时间点上样本的平均值。我们写了一篇论文投给某国际期刊，有位评审人要求我们随机抽取10人，在同一图里显示各自的growth curves。我们在SPSS中试了很久，怎么也无法制作这种图。不知是否可以在SPSS中“自动”做到？

庄主 @ 2010-04-18:

最近我教的统计课里，也有一位同学提出相同的问题，其答案在于纵向数据的特殊结构。一般说来，纵向数据的结构有“矮胖型”和“瘦长型”两种。但你们需要的是第三种结构。

矮胖型数据与更常见的横向数据相似，每一列是一个变量、每一行是一个个案，由于纵向数据的因变量有多个时点的观测值，每个观察值被当做一个变量，分别占领一列，一般在因变量名后加下标1、2、…、t（t=时间点个数）来显示各自的观测时间点。所以，这种结构的正式学名叫做“multivariate format”（因变量多列型）。如表一代表你们的数据，其中Y1、Y2和Y3是因变量Y在三个时间点上的观察值，注意它们是被当做三个变量分别各占据一列，X是自变量（只测量一次，所以只有一列）、最后的“…”表示还可以有其它自变量。GLM、SEM等都是使用这种结构的数据。但是，这种数据无法用来制作“intrapersonal growth curves”。

表一、因变量多列型数据结构（n行记录、t列因变量）

ID	Y1	Y2	Y3	X	...
1	y11	y12	y13	x1	…
2	y21	y22	y23	x2	…
…	…	…	…	...	...
n	yn1	yn2	yn3	xn	…

在瘦长型结构中，因变量只占一列，但是每个个案占三列，因此因变量y1、y2和y3分布在这三行之中（见表二）。为了保留Y的观测时间点，新增加了一个变量Time，取值1、2、…、t。这种结构的正式学名叫做“multirecord format”（个案多行型），是HLM和其他多层分析软件所要求的数据格式。在这种数据结构中，你可以通过选择个人的ID来显示一个人的增长曲线，但也无法在同一图中显示多人的增长曲线。

表二、个案多行型数据结构（n x t行记录、1列因变量）

ID	Time	Y	X	…
1	1	y11	x1	…
1	2	y12	x1	…
1	3	y13	x1	…
2	1	y21	x2	…
2	2	y22	x2	…
2	3	y23	x2	…
…	…	…	…	…
n	1	yn1	xn	…
n	2	yn2	xn	…
n	3	yn3	xn	…

如要在同一图中显示多条增长曲线，需要将矮胖型或瘦长型数据转换成第三种结构，这在文献中还没有专门的名称，我姑且称之为individuals-as-variables format（“每人一列型”），如表三所示。这种结构更加“奇怪”，每一列是一个人的因变量或自变量，而每一行是一个时间点。本例t = 3，所以只有三行，比起矮胖型的n行来更加矮胖了。这种结构不适合做统计分析，但十分适合做各种图形，如可以做以Time为X-轴、单个或多个Y为Y-轴的增长曲线，也可以做以X为X-轴、Y为Y-轴的个人层面X-Y散点图。

表三、每人一列型数据结构（t行记录、n列因变量）

Time	ID1_Y	ID1_X	ID2_Y	ID2_X	…	IDn_Y	IDn_X
1	y11	x1	y21	x2	…	yn1	xn
2	y12	x1	y22	x2	…	yn2	xn
3	y13	x1	y23	x3	…	yn3	xn

好了，根据上述原理，你可以按需要而将数据在这三种结构之间互相转换。当然，如果你会使用SPSS的Syntax指令，确实可以用以下（或类似）的指令来“自动化”操作（注：指令中的大写字母是SPSS指令、小写字母是可以替代的变量名或文件名）。

*1. 假定你的数据是矮胖型结构，首先转换成瘦长数据.
VECTOR j=y1 to y3.
LOOP i=1 to 3.
COMPUTE y=j(i).
COMPUTE time=i.
XSAVE OUT 'r:\temp.sav'/KEEP id time y x.
END LOOP.
EXE.

*2. 随机抽取10个个案.
SAMPLE 10 FROM 100.  
EXE.
MATCH FILES FILE */KEEP id.    /*只保留被抽取的id.
AUTORECODE id/into newid.      /*对id重新排序.

*3. 与瘦长数据并行对接.
MATCH FILES TABLE */FILE 'r:\temp.sav'/BY id.
SELECT IF newid>0.     /*剔除没有newid的个案.
EXE.

*4. 从瘦长数据中逐个提取个案，分别保留到单独文件中.
DEFINE !newcase (!POS, !CMDEND).
!DO !i !IN (!1).
TEMP.
SELECT IF newid=!i.
SAVE OUT !QUOTE(!CONCAT('r:\newcase', !i, '.sav'))
  /KEEP time y x
  /rename (y=!concat('y', !i)/rename (x=!concat('x', !i).
!DOEND.
!ENDDEFINE.
!newcase 1 2 3 4 5 6 7 8 9 10.
EXE.

*5. 将10个单独文件平行对接起来，构成最后的“个案每列”结构.
MATCH FILES FILE 'r:\newcase1.sav'
  /FILE 'r:\newcase2.sav'
  /FILE 'r:\newcase3.sav'
  /FILE 'r:\newcase4.sav'
  /FILE 'r:\newcase5.sav'
  /FILE 'r:\newcase6.sav'
  /FILE 'r:\newcase7.sav'
  /FILE 'r:\newcase8.sav'
  /FILE 'r:\newcase9.sav'
  /FILE 'r:\newcase10.sav'.
EXE.

*6. 打印10个因变量对时间的散点图.
TSPLOT y1 y2 y3 y4 y5 y6 y7 y8 y9 y10/ID=time.

以下是步骤6制作的10条“个人增长曲线“图，估计就是你们要画的那种了。

如何处理自变量之间的相关关系？

JF @ 2010-03-15:

我有一个初级问题想了很久还是不清楚。假如我有一个因变量Y、两个自变量X和Z，如果做回归分析，只要将X和Z同时进入回归模型就可以了，不需理会X和Z的相关关系。但是如果用SEM，除了要分别连接X和Z对Y的路径，还要连接X和Z之间的相关关系。这是为什么呢？不是说在结构层面回归和SEM是一致的吗？

另外，在报告上述SEM结果时，是否需要描述和解释X和Z的相关关系？如果用回归分析，是否还需要另行计算X和Z的相关关系、然后再报告呢？

庄主 @ 2010-03-20：

你的问题确实简单、但绝非初级，因为其中涉及了回归分析与结构方程模型（SEM）的主要异同，值得讨论一下。首先，自变量与因变量之间的结构关系 (structural relationship among variables)，如自变量对因变量的直接影响、间接影响、总影响、交互影响、等等，在回归和SEM中都是同义的（但不一定是等值的，因为前者含有测量误差而后者不含测量误差，但这与本文无关，所以下面的讨论均假定所有变量都不含测量误差）。

但是，在处理自变量之间的相关关系时，两者所用的方法不同：回归是用隐含方法而SEM是用明示方法。在回归模型 Y = b₀ + b₁X + b₂Z中，对回归系数b₁和b₂的估算公式分别包含了X与Z的相关系数（记为r_XZ；同理，Y与X、Y与Z的相关系数分别记为r_YX和r_YZ）:

和

由于b₁和b₂是在Y与X或Z的简单相关系数中扣除了X与Z的相关程度（以及Y与另一自变量的相关程度），所以b₁和b₂又被叫做partial regression coefficients（偏回归系数）。可见，在回归分析中，自变量之间的相关关系是自动而且必须地被控制了的。这里的“被控制”是指用于消除自变量之间的相关关系的影响。

在SEM中，自变量之间的相关关系是需要明确设置的。如在使用矩阵语言的LISREL中，通过指令"FR PH (1, 2)”来估算r_XZ；而在使用图形语言的AMOS中，则是通过在X和Z之间画一条双箭头的曲线来估算r_XZ（见下图，注：图中的三个参数b₁、b₂和r_XZ是不需要的，这里只是为了说明它们与上述回归模型的对应关系）。

该SEM模型与上述回归模型是等价等值的。大家可以用一个含三个变量、N > 200 （SEM所需的最小样本量）的数据验证一下，两个模型的b₁、b₂、r_XZ、R-Square（= AMOS中的MSC）、Std error of the estimate（= SEM中e的Variance的平方根）应该都相等。然而，回归用的是OLS（最小二乘法）而SEM是用ML（最大似然法）来估算上述参数的。这两者之间的差别，除了对样本量的要求不同（ML估算只有在大样本条件下才可能接近OLS结果），还有许多深层的差别。这里只讲其中比较明显的一个差别：如上所示，r_XZ在回归中是自动被控制起来的，但在SEM中却需要人为设置。反过来说，如果需要的话，在SEM里也可以设置r_XZ = 0（在AMOS中也可以将X和Z之间的曲线删掉）或其它任意值（1.0，0.5，等等）。如此设置的模型，因为少估算了一个参数，所以会比原模型多出一个df（自由度），通过比较两个模型的拟合指数（Chi-squares）之差，就可以检验 r_XZ = 0（自变量之间为正交）或r_XZ = 1 （自变量之间没有discriminant validity）等假设。这些都是无法在回归分析中实现的。

回归模型与SEM模型之间更核心的区别在于前者是在变量层面检验自变量对因变量的解释程度、而后者则是在观察值的方差-协方差矩阵层面检验理论模型与实际数据之间的拟合程度。打个不完全恰当的比分，回归是西药，针对特定病症有强效，但不顾其它后果；而后者是中药，旨在整体和治本，但有时对特定病症并无速效。这种根本区别在本文讨论的自变量相关关系上也有一定影响，但这是一个大题目，需要很多基本概念和铺垫，否则难以讲清，所以不予展开，只是提醒大家，SEM的水很深，下水前要做足热身运动，而回归则是最好的热身运动。就如现在的中医学院都是先教西医原理、再进入中医的。

回到你最后那个问题：如何报告r_XZ？一般说来，自变量之间的相关关系（如r_XZ）是一种unanalyzed relationship（不作分析的关系）。这里的所谓“不作分析”指的不是统计分析、而是理论分析。如上所说，r_XZ在回归中是不直接计算的，但在SEM和用回归做路径分析中均需要统计分析的。但是，除非有特定研究目的（如上述检验自变量之间的discriminant validity）之外，大多数理论并不规定自变量之间关系的强度、方向（谁影响谁）、性质（正或负相关）等，所以实际研究中往往只是简单地估算它们之间的相关关系而不进一步深究其关系的性质、方向、性质等。在写报告时，如果用图形表示实证模型的话，可以在图上标出相关系数的估计值；如无图形，可在附录或注释中用文字或表格报告一下；但在正文中则一般不必提及。

清华SEM班邀请外校学生网上实时参与

课程名称：结构方程模型的原理与应用 Structural Equation Modeling: Principles and Applications

对象：清华大学新闻与传播学院硕博研究生及外校新闻传播院系本科1-3年级或硕士研究生1年级同学20人

时间：2010年5月15-24日

报名：2010年3月31日止

详见：http://www.tsjc.tsinghua.edu.cn/news.php?id=971

如何确定两个调节变量之间的主次关系？

SJ @ 2010-03-02:

祝老师您好！我是心理系的学生。在网上偶然逛到您的庄园，受益匪浅！非常感谢您的慷慨，跟大家分享您的所学所得。我最近在处理早前的一个数据，遇到困惑，不知道该怎么继续，想向您请教，先谢过。

我的数据涉及以下变量：一个自变量、一个因变量、四个假设的中介变量。另外人口统计学变量方面，考察了年龄（分成四个年龄组）和性别。我关注的是自变量如何通过中介变量影响因变量，以及这种影响是否存在年龄的发展差异。然而，我在做各个变量的相关时发现，性别跟好几个重要的变量都有显著的相关。因此我的困惑在于，我应该如何处理性别的问题。1.把性别作为调节变量，放到各个年龄组中来建立模型？2.还是每个年龄组都建立男生模型和女生模型？您觉得哪种方法更合适？具体又该怎么操作呢？

庄主 @ 2010-03-06:

谢谢与大家分享你的研究问题。这是一个相当复杂（其复杂程度应该远远超出你的预计，具体见下）的研究设计。我前天在我的课上介绍了你的问题，建议学生们来这里分享他们的看法。至今还没有人现身，也许是你的问题太难、也许是他们还没完成下周一交的作业。我先说一下解决方案的基本思路，希望他们能够接下去帮你解决方案的操作问题（同学们，这是你们给老师和学校挣面子的时候了）。

先整理一下你的问题所涉及的研究假设：

H1. 自变量X对因变量Y的直接影响（记为b_YX）。

H2. X通过中介变量M1-M4对Y的间接影响（分别记为b_Y(M1-X)、b_Y(M2-X)、b_y(M3-X)和b_Y(M4-X)）。

H3. 年龄A对直接影响b_YX的调节作用（即A与X对Y的交互效应，记为b_Y(X*A)）。

H4. 年龄A对间接影响b_Y(M1-X)等的调节作用（即A与X-M对Y的交互效应，分别记为b_Y((M1-X)*A)、b_Y((M2-X)*A)、       b_Y((M3-X)*A)和b_y((M4-X)*A)。注：因为X-M对Y是中介关系，所以A与它们的交互关系是一种被称为“moderated mediation“、即“被调节的中介关系”，相当复杂！）。

先在这里停一下。H1-H4可以用OLS回归来分析，但在SEM工具（如LISREL、AMOS等）中更方便。如用后者，需要把年龄当做组别，而将样本按年龄分成4组、通过比较组间的invariance来检验X对Y的直接和间接关系是否随着年龄的变化而不同（具体操作这里略过）。也就是说，moderated mediation关系，听起来很复杂，但在SEM中通过设置组间equality constraint的小技巧（或“小伎俩”？），很方便就能解决了。

好了，回到你最后的问题：如何检验性别S的影响？也就是检验以下假设：

H5. 性别S和年龄A对直接影响b_YX的调节作用（即S、A与X对Y的交互效应，记为b_Y(X*A*S)或b_Y(X*S*A)）。

H6. 性别S和年龄A对间接影响b_Y(M1-X)等的调节作用（即S、A与X-M对Y的交互效应，分别记为b_{Y((M1-X)*A*S)} 或      b_{Y((M1-X)*S*A)}等）。

你考虑了两种方案来检验H5和H6：一是将性别nested（嵌镶）到年龄中、二是将年龄嵌镶到性别中。表面上看，好像两者有根本区别，但实际上是一回事！性别和年龄是两个同等级别的调节变量，它们的联合影响是一种3rd-order interactions（三阶交互效应，也相当复杂），用公式来表述，如H5中的b_Y(X*A*S)或b_Y(X*S*A)，前者是年龄嵌镶在性别中、后者是性别嵌镶在年龄中，但无论谁嵌镶到谁中去，b_Y(X*A*S)和b_Y(X*S*A)两者是完全同价等值的。如果用SEM来检验，也无论谁嵌镶到谁中，你总需要将样本分拆成8个组（4个年龄组X2个性别组）。当然，在解读结果时，你可以而且需要根据自己的理论框架来确定A和S之间谁主谁仆的次序。

最后，要说一下检验如此复杂模型的成本问题。如上所说，如果用SEM，需要8个组；基于每个组涉及5个自变量（X、M1-M4），按每个自变量需要20个案来计，你至少需要每组100个案，总样本800个案。当然，你的年龄组分布可能不均匀，所以总样本很可能要1000以上。如果不用SEM而用回归，可以不分组，但是变成了一个非线性模型，涉及了24对二阶交互关系和12对三阶交互关系，即使总样本有1000个案，也只少不多。样本数少了、会有什么后果？你的中介效应、调节效应和被调节的中介效应都有可能不显著。其中的最薄弱环节是中介效应（H2）。所以，建议你先将H2分成H2a-H2d四个分假设，分别检验A和S对各分假设的调节作用（= 4 X  (4 X 3 /2) X 2 = 48个组间比较，如果你想不通为什么会有48个组间比较，请详细演算一下），以简化模型。

总结：中介效应、调节效应和被调节中介效应在理论上都是很吸引人的模型，但在实证上即昂贵又难操作，需要事先有充分的思想和技术准备。

如何理解SEM的八个参数矩阵与七种变量之间的对应关系？

s @ 2010-02-05:

 

曾看过你的帖子“LISREL的八个矩阵”，最近在学习用AMOS做SEM分析，不知两者有何关系？

 

庄主 @ 2010-02-15：

 

如我在上述帖子中说的，LISREL是用八个矩阵来设置SEM模型的。这些矩阵分别代表了SEM模型中七种变量的参数。在LISREL中，变量与参数之间的对应关系是比较明确、不易混淆的。如，大家知道，描述因子与其测量指标之间关系的参数叫做“因子负荷”，其中外生因子测量指标x的负荷矩阵是用Λ(x)来估算、内生因子测量指标y的负荷矩阵是用Λ(y)来估算的，两者不能放在一起（即外生因子无法与y相连而内生因子无法与x相连）。这种规定在大部分情况下是合理和必要的。（当然，少数情况下，研究者也许有特殊理由需要将x挂到内生因子上或y挂到外生因子上，就需要设定特殊的“All-y model”（全y模型）。这种额外步骤，虽然麻烦，但防止了初学者因不知情而乱点鸳鸯谱。）

 

AMOS是通过图像来设置模型的，用户不再需要与八个矩阵的希腊字母打交道，所设置的模型是“What you see is what you get”（WYSIWY），很容易上手、也避免了模型设置时的一些常见错误。但是，在这种“自由自在”的界面中，很容易犯一些LISRE里不会出现的错误。比如上面所说的，任意（或根据Modification Index的误导）将x挂到内生因子或将y挂到外生因子上去。这种模型或者无法identified、或者违反“误差项与自变量独立”的基本假定，因为AMOS以及其它SEM软件在估算模型的参数时，其实还是在背后使用上述矩阵。

 

为了帮助大家在用AMOS设置模型时避免设置不能或不该估算的参数，我在八大矩阵的基础上再做了一个表（见下），以显示八个参数矩阵与七种变量之间的关联与隔离：

 

 

表三的7列和7行分别代表了SEM的七个变量（包括外生因子ξ、内生因子η、η的误差ζ、外生因子的测量指标x、内生因子的测量指标y、x的误差δ、y的误差ε），它们在列里担任的是自变量的角色、而在行里担任的是因变量的角色。

 

两种变量相交的格里如果出现一个希腊字母，就说明它们之间存在一个参数矩阵（在下图中用黑色线条来表示）；而如果是个空格，就说明它们之间不能发生关系（在下图中用红线表示）。如第一列ξ与第一行ξ之间有个方差-协方差矩阵Φ（如下图中的φ₁₂）；第一列ξ与第二行η之间有个外生因子->内生因子的回归系数矩阵Γ（如下图中的γ₁₁和γ₂₂）；第二列η与第一行ξ之间是空白（即图中η₂到ξ₁的错误红线），因为内生变量不能影响外生变量（AMOS是可以让你画这条线的，但这在逻辑上是错的）；当然第二列η与第二列η之间是可以有一个内生因子->内生因子的回归系数矩阵Β（如图中的β₁₂和β₂₁）；等等。

 

表中还有三个记为“I”的矩阵，它们不在八个矩阵之内，而是三个对角线为1、其余部分为0的Identity矩阵，用来定义三种误差项变量（ζ，δ和ε）系数的数学工具，而AMOS在处理误差项变量系数时则是很“智能”的，会在相应处自动为它们标出取值为"1”的回归系数（见下图）。

 

LISREL的八个矩阵

(原版2007年5月19日，略有修改重发)

传说中的“八大军区联络图”终于出笼了：

上图看起来挺吓人的。别紧张，先定义一下。图中每个圆圈代表一个隐含因子、每个方块代表一个观测变量、每条直线或曲线代表一个参数（parameter，也叫系数）、跟在每条半封闭直线后面的是一个因子或变量的残差（error）。所谓“八大矩阵”，就是八种参数的集合。分别列在表一：

如表所示，其中前四个矩阵用于测量模型部分、后四个矩阵用于结构模型部分；每模型一部分又分别分为外生（即图一的左边）和内生（图一的右边）两边；每一模型部分的每一边，再分别分为关系参数和残差参数。即一个2 X 2 X 2的设计，十分严密。

上面的图和表中，都用到了希腊字母、而且大小写并用，实在是三难（难认、难读、难记，读音参见表二）。其实经典统计学中也用到一点希腊字母，其规则是：变量名用罗马字母（即英文）、参数用希腊字母（如回归系数叫BETA）；总体变量和参数用大写、样本变量和参数估计值用小写。LISREL大体上沿用了这些规则。然而，由于SEM中的变量有观测的和隐含的之分，LISREL的创始人Joreskog决定沿用罗马字母表示观测变量、但用希腊字母表示隐含因子。其用意可嘉、但结果使得参数和隐含因子分享同一套符号而产生了很多困扰。（如果该老友用禅经字母来表示隐含因子、那该多爽啊。）

八大矩阵是LISREL的核心思想，也是其与AMOS、EQS等其它软件的主要不同。其缺点如上所说，概念太多、名字难念、令人望而生畏。优点嘛，则见仁见智。我用了近20年，觉得其好处主要有两个：：一是便于区分外生因子（exogenous factors）与内生因子（endogenous factors）之间、隐含因子与观测变量之间、以及因子/变量的各种相关系数之间的差别；二是便于用户之间交流（包括写学术报告）时有一套确定而又简便的符号系统。

当然，是否值得仅仅为了这些好处而去重学一种外语（希腊语），则又是见仁见智了。我的看法，如果你用LISREL，那只能学；如果你用其它软件、但有志成为SEM的pro，那也要学一下（不然如果与主流沟通？）；如果你用其它软件而无意成为SEM方法专家，不学也罢，有所失必有所得。

如何识别回归分析中的压抑效应？

DHF @ 2010-01-25：

祝老师，您好，我是心理学专业学生，想向您请教一下，如何identify a variable as a suppressor variable in regression analysis? 我的数据中出现了类似于classical suppression的效应，但不清楚IV的regression weight提高多少才可以认为是suppression effect. 多谢！虎年顺利！

庄主 @ 2010-02-06:

Suppression effects（压抑效应）是回归分析中的一个重要而又复杂但却不常见的概念。你提到classical suppression（经典压抑），自然也知道此外还有net suppression（净压抑）和cooperative suppression（合作压抑）。相比之间，经典压抑最罕见（以下会谈到），但最容易确认。我用模拟方法做过经典压抑数据，但在实际研究中从来没有遇到过这种数据。你好像中了彩票，值得庆贺。如不怕泄露学术机密，不妨描述一下你的数据以及你认为可能的原因。我相信很多读者都会有兴趣了解。

考虑到大多数读者可能对压抑效应知之甚少，我先讲一些基本概念（估计你已经知道其中的大部分）。

为了便于叙述，我们只讨论含有两个自变量的回归模型，即 Y = B₁X1 + B₂X2。其中，B1和B2是标准化回归系数，所以没有常数项），另外记X1与Y的相关系数为r_y1、X2与Y的相关系数为r_y2、X1与X2的相关系数为r₁₂。 习惯上一般将X1看做主要的自变量而将X2看做是压抑变量。当然，X1和X2是对称的，完全可以将X1看做压抑变量的。

统计文献中有过不少压抑效应的定义，其基本思想基本一致，但具体公式上有所不同（所以结果也略有不同，但我不准备涉及那些技术细节）。就基本思想而言，压抑效应是根据r_y2 与 B2之间（或者r_y1 与 B1之间）的差别来确定的。具体说来，r_y2 可以取正值、负值和零值三种可能性，B2则有正值和负值两中可能（但B2不能为零，详见下文）。这样我们就要3 X 2 = 6种情况，分别属于经典压抑、净压抑和合作压抑：

1. r_y2 = 0而B2 > 0，叫做 positive classical suppression（正向经典压抑）；
2. r_y2 = 0而B2 < 0，叫做 negative classical suppression（反向经典压抑）；
3. r_y2 > 0而B2 > r_y2 ，叫做 positive cooperative suppression（正向合作压抑）；
4. r_y2 < 0而B2 < r_y2 ，叫做 negative cooperative suppression（反向合作压抑）；
5. r_y2 < 0而B2 > -r_y2，叫做 positive net suppression（正向净压抑）；
6. r_y2 > 0而B2 < -r_y2，叫做 negative net suppression（反向净压抑）。

上述六种情况，都包含|B2|>|r_y2|的条件，即一个自变量的回归系数之绝对值必须大于其与因变量的相关系数之绝对值。这是压抑效应的必要和充分条件。这里的“大于”、“等于”、“小于”、“差别”等，都是在统计显著性检验的含义上说的。如，在一个样本中，r_y2的值可以不是0、而是一个与0没有显著差别的数值（当然是一个很小的数）；而B2绝对值与r_y2绝对值之间的差别一定要达到统计显著水平（至少为p < 0.05）。当然，如何进行这种统计检验则不是一个容易的事，因为检验H0：|B2|=|r_y2|的零假设，需要有B2和r_y2的联合标准误差SE_B2,ry2，而无论相关分析和回归分析都无法计算SE_B2,ry2。

所幸的是这种困难对于经典压抑并不存在，因为根据定义，经典压抑的前提是r_y2 = 0，所以检验经典压抑只须证明当r_y2 = 0时，|B2| > 0（即上述情况1和2）。这大概就是你想知道的答案了。这么简单？是的。至今为止我看到的所有文献 都是这个意思。当然，|B2| > 0 仅仅表明B2有统计意义上的显著压抑效应，至于这种压抑效应是否具有实际或理论意义，则取决于B2的大小。这时，我们可以按判断回归系数大小的传统标准（如0.1为弱、0.3为中、0.5为强）来解读B2的压抑效应。

虽然我们无法对净压抑和合作压抑的零假设做正式的统计检验，但我们也可以援引上述rule of thumbs（惯例）来解释|B2|-|r_y2|的大小。（我在写这个帖子时，突然想到，也许这个问题可以在SEM中通过equality constraint的方法来解决。我一下子没想好，如有进展，会在这里报告。）

最后再补充一下：所谓“压抑效应”，是指上述回归模型因为引入了X2而将X1的方差中与Y无关之部分压抑或过滤掉了，从而改进或提高了该回归模型对Y的解释力。(The inclusion of X2 in the regression model suppresses or removes the part of variance in X1 that is unrelated to Y, which results in enhancement of the explanatory power of Y by the model.) 早年（也许是由于计算能力的局限），很多研究建立在相关分析基础之上，所以很有必要关注压抑效应的可能性。现在，多元回归分析是很多研究的起点。既然回归模型中已经同时考虑了X1和X2对Y的影响，那么X2的压抑效应已经被过滤了（当然也许还有X3、X4等等的压抑效应没有被过滤掉）。再加上压抑效应的数据不常见，所以现在很少人会检验压抑效应。但是，如果数据中真有压抑变量，其成因是很有价值的问题，弃之不顾太可惜了。同时，压抑效应的知识还可以帮助我们在研究设计阶段（即收集数据之前）将表面上与Y无关但与X1有关的X2包括在问卷或其它数据采集工具中。

如何比较一个自变量对三个因变量的影响大小？

ZYS @ 2010-01-23:

Dear Dr. Zhu,

I read your blog post on how to test the differences of two correlation coefficients posted on http://zjz06.spaces.live.com/blog/cns!3F49BBFB6C5A1D86!954.entry. Is it appropriate to use your method for two regression models based on one sample population?

My question is whether there is a appropriate way to test significant difference between regression coefficients of two different models from same sample population? For example in the below table, how would we statistically compare the difference between betas for political interest as predictors of DV in three conditions? This is a repeated measure experiment. the same group participants participated in three conditions in three months. In other words, the research question is whether the impact of political interest on opinion expression is moderated by condition... The reviewer wants a statistical test --but i didn't find a good way to test since they are not independent samples...

	Opinion expression in Condition 1	Opinion expression in Condition 2	Opinion expression in Condition 3
	ß	ß	ß
Education	.13*	-.07	-.06
Male	.10*	-.01	.05
Age	-.04	.28***	.31***
White	.04	.03	-.03
Political Interest	.33***	.10*	.08
R-square	.04	.09	.11
F	3.60**	7.48***	9.61***

Is there a better way this problem could be tackled?

庄主 @ 2010-01-24:

Your research question differs from the one in that post, where the issue is to compare the correlation coefficients between two independent variables (IVs) with the same dependent variable (DV) whereas your task is to compare the correlations between the same IV with three different DVs.

One approach you can consider is repeated measures regression in general linear modeling (GLM), in which you form a within-subjects (WS) factor to account for the three DVs, and then regress the WS factor on your IV and control variables.  To test the significance of the differences among the relevant regression coefficients, you use the procedure described in 如何检验两个回归系数的差别？.

Another approach, which I think simpler and easier to be understood, is to test a path model with  equality constraints in SEM (see the diagram below). Aside from your regular hypotheses, you fit a series of nested models to test the null hypothesis that β₁ = β₂ = β₃. For example, you compare the fully unconstrained model in which β₁, β₂, and β₃ are free to be estimated and the fully constrained model in which β₁, β₂, and β₃ are fixed to be the same.  The difference in the resulting Chi-squares between the two models, tested with Chi-square distribution with 2 degrees of freedom, tests the above null hypothesis.  In addition, you can test the fully constrained model with three partially constrained models, each with a pairwise constraint such as β₁ = β₂, β₁ = B₃, or β₂ = β₃, to entertain the possibility that not all three coefficients are exactly the same but some pair(s) of them may be. 

With the data in the table you provided, I guess that Condition 1 would be significantly different from Conditions 2 and 3 whereas the latter two might not. 

Good luck with your publication.  If it’s published, please come here to share your experience in getting published in journals.  Many readers of this blog would be very interested in learning from your experience.

如何解读回归与ANOVA的不同结果？

Anonymous @ 2010-01-22:

祝老师好！我是心理专业的学生，想请教一个具体的问题。对一个三类别变量作ANOVA结果显示类别1显著小于类别2和类别3，但将这三类转换为dummy variable，类别1为00，类别2为01，类别3为10，用同样的因变量来做回归时，结果是第一个dummy variable没有显著差异，而第二个dummy variable有显著差异，这是不是意味着类别2显著区别于类别1和类别3呢？如果是，为什么会出现这种结果呢？可能需要加上的是我在做回归时还引入了一些其它的变量，其中有一个会与类别变量有相关。

庄主 @ 2010-01-24:

将一个含3个类别的名目变量转换成两个dummy variables（分别记为D1和D2）后做回归分析，D1反映的是类别1和类别2的差别、D2反映的是类别1和类别3的差别。那么为什么类别1和类别2的差别在ANOVA中显著而在回归中不显示？因为你在回归中加入了其它自变量而成为多元分析而ANOVA是只有一个自变量的单元分析。其实，你可以将那些新加的自变量作为协方差 (covariates) 放入ANOVA的，这时就成了ANCOVA (Analysis of Covariates)，其结果应该与你做的回归分析完全一样。

你再问：D2为显著，是否说明了类别2显著区别于类别1和类别3呢？没有。D2只说明类别1和类别3的差别，与类别2无关。D1检验类别1与类别2的差别。如果希望知道类别2与类别3的差别，将类别2设为基准组（即类别2取00值，而类别1为10值），那么D2就是反映类别2与3的差别了。

如何检验交互效应的显著性？(更新版)

yxf @ 2009-12-29:

庄主您好：我是一名博士生，怀着非常忐忑的心情给您写这篇文章。我经常拜读您竹家庄上的文章，受益很深。您在2009年4月11日文章“如何绘制调节效应的图形？”，我能够看懂，但是用您的绘制调节变量的图形的方法于下面这篇文章得出的回归系数，和该文章得出的回归系数，为何不同？

这是发表于《管理世界》2009年第一期的一篇文章（下面复制了它的两个图和一段文字）。

首先，根据您的绘制调节变量图形的方法，

Y = 0.405X + 0.360Z - 0.186XZ + 常数 =（0.405 - 0.186Z）x + 0.360Z+常数

（1）低中国人传统性，取Z为均值减一个标准差，为-0.647，此时Y = [0.405 - 0.186 × (-0.647)]X + 0.360 × (-0.647) + 常数 = 0.525X+常数

（2）高中国人传统性，取Z为均值加一个标准差，为0.647，此时Y = [0.405 - 0.186 × (+0.647)]X + 0.360 × (+0.647) + 常数 = 0.525X + 常数 = -0.285X + 常数

但是，为什么这篇文章得出的结果不同呢？

（1）低中国人传统性，Y = 0.503X + 常数 （p＜0.01）

（2）高中国人传统性，Y = 0.018X + 常数 （p＞0.01）

这篇文章的结果正确吗，它是如何计算出来的，特别是它的p值是如何计算出来的？是不是我没有正确领会您的“如何绘制调节效应的图形？”的内涵？

（庄主注：yxf的信中附有原文的部分页面，因涉及版权，这里删去。有兴趣者请参阅：汪林、储小平、倪婧：“领导—部属交换、内部人身份认知与组织公民行为”,《管理世界》2009年第1期，97-108页。)

庄主 @ 2009-12-30：

你提了两个问题。一是如何计算“低传统”组和“高传统”组各自的回归斜率；二是如何检验这些斜率的统计显著水平？以下分别简答之。

一、如何计算分组回归斜率（也叫“简单斜率”）？我在多个前贴（包括你提到的“如何绘制调节效应的图形”一文）中已介绍过，简单斜率是根据总样本回归模型

Y = b0 + b1X + b2Z + b3XZ                 (1)

而计算出来的。即先选定若干个Z的值（如本例中小于和大于“传统性”均值的一个标准差，分别记为Z1和Z2），然后代入公式1，就有

Y = b0 + b1X + b2Z1 + b3XZ1 = (b0 + b2Z1) + (b1 + b3Z1)X            (2)

和

Y = b0 + b1X + b2Z2 + b3XZ2 = (b0 + b2Z2) + (b1 + b3Z2)X             (3)

其中b1+b3Z1是低传统组的简单斜率、b1+b3Z2是高传统组的简单斜率。这种方法，与论文作者所参照的Aiken and West (1991)的方法是完全一样的。

至于具体计算，只是做简单的加减乘，没有特别深奥的地方。当然，先要弄清Z1和Z2是原始数据还是取中值 (centered score)。在本例中，前者为3.52±0.647而后者为±0.647（因为取中值的均值为0）。你是用后者来计算的，你的结果中低组的斜率是对的（0.525），但高组的斜率错了，应该也是正数（0.285）而不是负数（-0.285）。我估计你算对但写错了。

作者为什么算出来分别是0.503和0.018？我看了原文，他们没有交代用的是原始数据还是取中值。如果用的是原始数据，结果应该分别是-0.129和-0.370，与其上下文不合。估计他们用的是取中值，但手算时出错了。你不妨直接写信问他们一下？

二、如果检验简单斜率的显著性？我在有关前贴中也应该讲过，但一下子查不出来，所以再讲一下。我们知道，一个回归方程的斜率（如b1），可以用t = b1/se_b1 来检验。同样，简单斜率b1+b3Z的显著性也是用一个类似的 t-检验来完成的（注意，要将这里的b1+b3Z当做一个常数来看），即

                          （4）

其中的分母就是简单斜率的标准误差，SPSS或其它统计软件不会直接报告这个参数，但可以根据以下公式

                    （5）

手工算出，其中的se²_b1和se²_b3分别是b1和b3的方差(variance)、cov_b13是b1和b3的协方差(covariance)（注意：这里提到的是b1和b3的方程-协方差而不是X和Z的方差-协方差），在SPSS中在Statistics的选项中选择“BCC”可以获得这些参数，而这里的Z则用上述的Z1或Z2值来代入。

算出公式4的t-值后，就可以查表得出其相对应的p-值了。估计原文作者就是这么做的。当然，他们如果报告一下两个t-值和对应的两个p-值各为多少，就更令人信服了。

yxf @ 2010-01-07

庄主，您好：非常感谢您的回复。我非常仔细地学习了您的“如何检验交互效应的显著性？”，感觉帮助非常大。在您的回复中，“二、如果检验简单斜率的显著性？”有一段话

“简单斜率b1+b3Z的显著性也是用一个类似的 t-检验来完成的（注意，要将这里的b1+b3Z当做一个常数来看），即公式4（省略），其中的分母就是简单斜率的标准误差，SPSS或其它统计软件不会直接报告这个参数，但可以根据以下公式5（省略）手工算出，其中的se²_b1和se²_b3分别是b1和b3的方差(variance)、cov_b13是b1和b3的协方差(covariance)（注意：这里提到的是b1和b3的方程-协方差而不是X和Z的方差-协方差），在SPSS中在Statistics的选项中选择“BCC”可以获得这些参数，而这里的Z则用上述的Z1或Z2值来代入。”

这里，se²_b1、se²_b3、cov_b13在SPSS中的计算方法我不太确定如何操作，因为不知道BCC是如何操作的？我找到两种方法，您认为哪一种方法算出的协方差是适合本文这里使用的，因为这两种方法算出的协方差不一致：

1. Analyze—>Regression—>Linear—>Statistics—>Regression Coefficients中 "Covariance Matrix” 打钩，然后算出协方差矩阵；
2. Analyze—>Correlate—>Biraviate—>Options中 "Cross-Product Deviations and Covariances” 打钩，然后算出协方差矩阵。

您认为哪一种方法是正确的，还是都不正确？正确的方法应该如何操作？

另外，“cov_b13是b1和b3的方差-协方差而不是X和Z的方程-协方差”，这两个协方差有何区别？

万分感谢！

庄主 @ 2010-01-16：

用方法1而不是方法2。如我原文中所说，前者是回归系数(b1, b2, b3）之间的方差-协方差、而后者是自变量（X, Z）之间的方差-协方差，是风马牛不相及的完全两回事。

大家应该对后者很熟悉，即使不那么熟悉、但在学习初级统计的相关系数部分时、多半也看到过相关系数与协方差之间的转换关系（Cov_xz = r_xzsd_xsd_z，即X和Z的相关关系r_xz乘上X和Z各自的标准差sd_x和sd_z就是X和Z的协方差Cov_xz）。很多学生对我说，他们的老师没有讲过这个公式。我的回答一般是“这还需要讲吗？”。比较一下相关系数的公式和协方差的公式，前者不就是少了sd_x和sd_z吗？甚至记不得公式，但一定知道相关系数是标准化的协方差、而协方差是非标准化的相关系数吧？将一个标准化的指标乘上其标准差不就是其非标准化的指标了吗？反之，将一个非标准化指标除以去标准差不就是标准化了吗？当然，如果只是通过老师的PPT讲义和点击SPSS菜单而学习统计的话（很可惜，现在的社会科学学生中大概99%是这么过来的），这些ABC原理都好像很陌生。青年朋友们：不要做PPT和SPSS的奴隶，多看书、并且经常手工演算各种公式吧。

那么前者呢？很可能你们老师们没有讲过。其实我的老师们（当中不乏顶尖学者）也都没有讲到，因为回归系数的协方差一般用不到。曾有一位美国名校名导师培养出来的博士朋友问我，b1和b3是两个常数、它们之间怎么可能有相关系数呢？是的，回归系数是常数，但任何统计量（常数）都有一个抽样分布（即假定从同一总体中抽取无数个相同大小的样本，做同一回归而得到的无数个回归系数就构成了一个服从t的抽样分布），在这个抽样分布中的每个回归系数都是一个变量（而不是常数），所以各自都有自己的方差、而相互之间就有相关系数或协方差。

为何回归方程的常数是负值？

L君 @ 2009-11-18:

老师，您好，我在做毕业论文。问题简化后说就是：有两个不同组别的多元线性回归方程进行比较

y1=a1+b1X1+c1X2+d1X3

y2=a2+b2X1+c2X2+d2X3

1，2为两个不同的大区域（每个大区域都有40个小区域作为观测值）；y为污染总量，X1, X2, X3为三种类型的污染源面积（工厂，工地，居民区），b, c, d为三种污染源的单位面积污染量（在模型里都为正数）。现在需要比较1，2两地的污染状况，三种类型污染源的污染贡献量等。我得到的两个回归方程，b、c、d都为正数，但是常数项a1为正，a2为负。这样对单位污染量的比较有影响吗？可以这么分析吗？在这个分析中，可不可以给出非标准回归系数的回归方程，然后用标准回归系数（常数项为0）解释贡献量？但是单位面积污染量要继续用于后续计算的话，是用标准还是非标准的回归系数呢？

但是，如果 y1＝30＋2X1＋3X2＋4X3、y2＝－300＋20X1＋30X2＋40X3，在两个区域，2区域的单位面积的效益就明比1大，但是在3类污染源面积相同的情况下，y总值是一样的？这个就不太好解释了。其实就算是都为正，但是相差较大的话，也不能比较区域1，2的单位面积效益大小？怎么解决这个问题呢？

还有，这个模型的R平方，还有sig等检验系数有的不合格。之后我改用偏最小二乘法，用SPSS和SIMCA-P计算结果都和多元线性回归得到的方程一样。那是不是随便用哪个结果都行呢？

庄主 @ 2009-12-06:

你提到了好几个问题，其中第一题：两个样本的所有自变量和因变量（污染值或面积）取值都应该是非负值、或许都是正值（960万平方公里之内哪里还有0污染的净土？），但是两个对应回归方程的常数项a1为正、a2为负。你问：这对样本之间“单位污染量”的比较有影响吗？我这学期教的同学中也有问过：“变量全部为正值、为什么回归方程常数为负值？我觉得后者问题更有普遍意义，所以本贴主要谈这个问题，你的其余问题放在最后简单说一下。

我们知道，常数项b0（你用a来表示，为了与本庄其它帖子一致，这里用b0）反映的是当所有自变量分别取值为0时因变量Y的值。但是，在很多实际研究中，出现负值的b0是一件很奇怪或很尴尬的事。在本例中，如果自变量X1-X3（工厂、工地、居民区）没有污染面积，那么该区域不仅没有任何污染而且还会“负污染”（世上真有比蓝天、绿地、白云更圣洁的境界？），真的很奇怪。其实，这仅仅是有关变量的取值区间及其关系强度之间的特定搭配而造成的错位而已。

我们先从下图中获得一些直观的认识。图中的两条线分别代表一个回归方程，其中A线是向上的（即b1为正），但它在X = 0时Y < 0（即b0为负）；相反，B线是向下的（即b1为负），而它在X = 0时Y < 0（即b0也为负）。说明b0的取向与b1没有直接关系。另外，A的数据可以局限在A1-A2范围内，即X和Y全部为正值；也可以局限在A3-A4范围内，即X和Y全部为负值。反之，B的数据可以局限在B1-B2范围内，即X为全为负值而Y全为正值；或者局限在B3-B4范围内，即X全为正值而Y全为负值。当然，如果数据局限在A2-A3或B2-B3范围内，X和Y即可为正也可为负。以上六种情况，穷尽了X和Y的可能取值，但其回归方程的常数b0总是为负，说明b0的取向与X和Y的取值范围也没有直接关系。

那么，b0的取向到底受什么影响？其中有什么规律可循？我查了一些教科书，希望找到一个权威的说法来引用一下，可惜还没有查到（也许我查的不够广泛和彻底）。以下是我的推导，尚未得到“权威”认可，仅供大家参考。

我们从简单回归方程出发：

Y = b0 + b1X             (1)

如重新组织公式1即有：

b0 = Y – b1X              (2)

我们知道，如果b1已知（通过回归分析而得知）、就可以将Y和X的任意一对常数（如两者的均值、最大值、最小值、均值之一个标准差之上或之下、等等）分别代入公式2而求出b0。这里，我们分别用Y和X的最小值（记为“Ymin”和"Xmin”）来代入公式2：

b0 = Ymin – b1Xmin   (3)

很显然，Ymin、Xmin和b1可以取任何值而公式3均可成立，这与我们从上图得到的直观理解是一致的。更重要的是，我们可以从公式3推导出b0取负值的条件：如果 b0 < 0, 那么Ymin – b1Xmin < 0, 也即 

b1Xmin > Ymin          (4)

或者，

b1 > Ymin/Xmin        (5)

公式4告诉我们，如果Ymin小于Xmin与b1的乘积，那么该回归方程的常数b0为负值；而公式5则直接显示，如果Ymin与Xmin的比值小于b1，那么b0为负值。（当然，我们将公式4和5中的“>”改成“<”或“=”，则可得到b0为正值或为0的条件，但因为后两者属于“正常”现象，所以不再赘言。）

好了，我希望大家至此明白b0为负实属正常情况，即不代表任何“负相关”、也不反映任何数据问题，而是我一开始说的那样：“有关变量的取值区间及其关系强度之间的特定搭配而造成的错位而已”。所谓“错位”，其实只是“错觉”而言。

当然，这种错觉有时很难向读者交代或解释清楚，尤其是在A1-A2数据的情况下，出现一个负b0总会令人质疑的。有何解决方法？有，很简单，就是对X取中值（centering，详见本庄前贴）。X取中值后，回归方程的斜率b1保持不变，但b0会变，其已经不再是X = 0时Y的值，而是X=均值时Y的值。如果数据是A1-A2段的话，那么X的均值一定是正的，所以b0也一定为正（见下图，其中A1’和A2’分别为A1和A2的取中值）。

最后简单回答一下L君的其它问题。

一、虽然你的a1为正、a2为负，但两个方程仍然是直接可比的。a1为正、a2为负的意思是，区域1的“污染起点”（即在没有受到X1-X3的任何影响下）高于区域2（也许因为还有其它污染来源）。当然，如果你对两个样本的X1-X3都取中值后，a1和a2应该全部为正，看起来好像更可比，但它们之间的差别应该与现在的差别完全一样。当然，取中后的a1和a2的解读有所变化，反映的是自变量X1-X3各自为均值（即工厂、工地和居民区平均污染水平）时该区域的污染总量。

二、比较两个方程，应该用非标准化回归系数（b）、而不是非标准化回归系数（Beta），因为b反映了X和Y的关系强度，而Beta则是用以下公式从b转换而来：

Beta = bSDx/SDy         (6)

其中SDx和SDy分别是X和Y的标准差。我们知道，两个样本之间的X或Y的标准差会因为各自样本大小、异常值（如区域1有一个超大的异常值或区域2有一个超小的异常值）等因素而不同，所以即使两个样本的b相等，它们的Beta也很可能不等。所以，比较不同方程之间的Beta是没有意义的。

如果你想比较X1-X3在两个区域的各自独立贡献(net contribution)，可以比较每个X与Y的semipartial correlation coefficient之平方（在SPSS回归中叫做PART）。

三、如果你的数据满足了线性回归（OLS）的要求，那么OLS回归的结果是“蓝色的”（best linear unbiased estimate，间称BLUE，即最佳无偏线性估计），所以应该报告OLS回归结果。

如何提高间接影响模型的效应？（更新版）

hz @ 2009-11-30:

我提出了一个理论模型（见下图），假设A通过B和C对D有间接影响。实证数据表明，A->B、B– C、C–>D的影响都显著，但是三者的乘积（即A–>D的间接影响）却不显著。另外，A–>D的直接影响也显著。不知有无方法提高间接影响？是否可以将显著水平从0.05放宽到0.10？

庄主 @ 2009-12-04:

你的理解对了一部分，即A–>D的间接影响包括A–>B–>C–>D的所有回归系数之连续乘积 (= 0.30 x 0.20 x 0.10 = 0.006)。但在你的模型中，A->D之间其实有三条间接路径：一是你说的A–>B–>C–>D；二是A–>B->D；三是A–>C–>D（见下图）。

如果你的理论规定A–>D的间接影响只能有A->B->C->D一条路径，是否可以？当然可以。但你须要预期到如此假设更难被证实。如果你的理论容许，那么加上A->B->D和A->C->D的间接影响之后会如何？一切取决于A->C和B->D的系数强度。你可以代入一些可能发生的数值来计算A->D的总间接影响。如，

1. A->B = 0.20和B->D=0.20，总间接影响=0.086，可能不显著，同时也小于A->D的直接影响；
2. A->B = 0.30和B->D=0.30，总间接影响=0.126，虽然仍小于A->D的直接影响，但可能显著，属于“弱间接影响”（参见前贴“如何检验两个中介变量的效应? ”http://zjz06.blogspot.com/2009/04/blog-post_25.html或http://zjz06.spaces.live.com/blog/cns!3F49BBFB6C5A1D86!1159.entry）；
3. A->B = 0.40和B->D=0.40，总间接影响=0.166，可能显著，并大于A->D的直接影响，属于“强间接影响”。

当然，基于你现有的回归系数均在0.10到0.30之间，我怀疑即使将后两条间接路径等间接影响（假定两个未知的系数也在0.10到0.30之间）加进去，总间接影响还可能不显著。总之，间接影响模型在理论上很诱人、但在实证上要求很高，尤其是多阶段间接影响模型，一般都很难证明。

最后，你问是否可以将显著水平条件放宽到0.10？答案是否定的。一、统计决策的显著水平（α）是在检验之前就要设置的，而不能在检验之后、因实证显著水平p大于α而将α提高。二、α一般设为0.05，代表犯Type I 错误的概念有5%，如果提高到0.10，则将Type I 错误提高到10%，除了初步的探索性研究之外，这种错误率太高。三、结构方程模型中的回归系数已经修正了测量误差，所以一般不应该再放宽其显著水平。

hz @ 2010-01-17:

在上次关于直接效应和间接效应的问题，我还有一个地方不明白：如何判断间接效应是在一定置信水平上显著？以A->B->C–>D为例，判断三者的乘积（即A–>D的间接影响）是否意味将A,B,C同时放入对D的回归方程，三者回归系数分别达到显著水平？

庄主 @ 2010-01-24:

文献上有过类似说法，但从未被证明过。现在一般的做法是用Bootstrapping求出三系数乘积 (如a x b x c)的standard error (如记为”se(abc)”) 的经验估计值，然后计算 abc/se(abc)的比率，该值也是服从t-分布的。AMOS里有Bootstrapping。

如何确定名目变量交互项的参照组是什么？

台灣吳同學 @ 2009-11-13:

老師您好,我是台灣的學生,對您的統計解釋相當有興趣。最近我遇到了一個問題,我嘗試把他說清楚,希望您可以幫我解惑。

在我的logit model裡頭,有兩個類別變數，分別為性別與教育程度。其中,性別是男女二分變數(男=1,女=0),而教育程度則分為低,中,高三類(中=0).我的依變數是收入,分為低與高兩種(低=0).假設,我想探討性別與教育程度的交互作用(性別X教育程度),我的交互作用項只能把1.男X低教育和2.男X高教育放入模型中,請問我的交互作用項在這時候的參照類是什麼?是1.男X中教育? 還是2.女X中教育?

另外,也想知道要如何解讀交互作用項B和EXP(B)的意義。希望您能看得懂我的問題,謝謝!

庄主 @ 2009-11-15:

吴同学，从统计上来说你的问题并不难，但要解释清楚却简短不了，而且有点绕弯弯（所以提醒读者随手做些推算验证，以免绕不出来）。我把这类问题叫做technically simple but practical not trivial (技术上很容易但操作上不简单)，往往会被人疏忽或轻视，所以不容易找到答案。如你问的，实质上是一个“如何解读回归分析中交互项的系数？”的问题，对此我已写过好几个帖子（如“如何在回归分析中检验和解读交互影响？”）。但是，你由于下面谈到的若干误解而对这个问题产生困惑，也许已问过其他人或查过其它参考文献，但却不得而知。

我觉得你的困惑可能有三个来源混合而成：第一，你的因变量(dependent variable)不是收入本身、而是高收入与低收入之比例的对数，但无论你根据什么理由来如此构建因变量，你的问题与因变量性质无关，也就是说交互项的对照组问题在包括OLS、GLS、Logit、Probit、Logistic等等所有回归分析中是一样的。所以有关如何解读回归分析交互影响的文献（包括我自己的有关帖子）都是直接相关的。

第二，你的两个自变量都是nominal scale (名目变量) 而不是更常见的interval scale (等距变量)，而且你用了dummy coding（哑变量编码）方法，但你对这种编码的原理了解不够（很多人都有同样问题），所以无法将如何解读定距变量交互影响的文献转换成你的答案。

第三，也许是最重要的，是你将交互影响等同于main effects（主效应）影响了。此话怎讲？你知道一个名目自变量转换成哑变量之后，其回归系数描述的是该哑变量取值为1的“研究组”与取值为0的“对照组”之间在因变量Y的平均值上的差别。这种理解完全正确。但是，你将其推广到对交互项系数的理解上去了，所以会问该系数是跟哪个对照组在比较？

为了有助其他读者理解你的问题，我用以下公式来表述你的回归模型：

Y = b0 + b1M + b2H + b3L + b4MH + b5ML                         (1)

其中，Y是因变量的平均值（注意：为了写作方便，本文没有按惯例在Y上加一横杆来代表平均值），M是性别（因为Male=1，所以命名为M），H是高教育程度（High），L是低教育程度（Low），MH是你说的“男X高教育”的交互项，ML是“男X低教育”的交互项。b0是在性别和教育两个变量中同时担任对照组（即同时取值为0）的FM（女性中等教育）组的均值，b1是男女差别（即性别的主效应，注意：这句话在有交互影响条件下有问题的，见后面的简单讨论）、b2是高教育与中教育的差别（高教育主效应，注意：这句话在有交互影响条件下也是有问题的，见后面的简单讨论）、b3是低教育与中教育的差别（低教育主效应）、b4是性别与高教育的交互影响、b5是性别与低教育的交互影响。

上面这段话中，大都分都是常识，唯一需要加以讨论的是什么叫做“性别与高（或低）教育的交互影响”。以b4为例，它反映的是“性别对高等-中等教育程度之间差别的影响”、或倒过来说，是“高教育对男女之间差别的影响”（这两种说法是等价的）。也就是说，b4描述的是高和中教育组之间的差别大小、在男性和女性之间是否相同；或者，男女之差的差别大小在高和中两组之间是否相同。这个意思，中文里说确实有点绕弯弯，用英文表述则相当清楚: b4 indicates whether the difference between the highly-educated and moderately educated groups is constant (uniform, equivalent, invariant, etc.) for men and women, respectively; or whether the difference between men and women is constant (…) for highly educated and moderately educated people, respectively. 

这是问题的核心：主效应系数（b1-b3）反映的是组间差别，所以有研究组和对照组；但是交互项系数（b4-b5）反映的是组间差别的差别（difference between diffrences between groups, or difference between group-differences)，所以没有主效应系数意义上的对照组。也就是说，b4或b5反映的不是两个组之间是否有差别，而是两个组间差别之间是否有差别，所以不需要有、也不可能只有一个对照组。

问题解决了吗？应该还没有。我希望大家能够记住两句话：一、交互项系数反映的是交互影响而不是组间差别（即“交互影响不等于组间差别”）；二、组间差别又是与（显著的）交互影响直接有关的。为了说明第二句话，我们来看看在交互项显著的条件下组间差别是如何计算的。我们可以根据模型1，写出计算你的六个组（= 2个性别组 x 3个教育组）的平均值Y的公式：（请大家拿出纸和笔来，将0和1值分别代入模型1，以复核实下述公式。光看不练，也许越看越迷糊。）

男高(MH):	YMH=b0 + b1x1 + b2x1 + b3x0 + b4x1x1 + b5x1x0 = b0 + b1 + b2 + b4	(2)
男中(MM):	YMM=b0 + b1x1 + b2x0 + b3x0 + b4x1x0 + b5x1x0 = b0 + b1	(3)
男低(ML):	YML=b0 + b1x1 + b2x0 + b3x1 + b4x1x0 + b5x1x1 = b0 + b1 + b3 + b5	(4)
女高(FH):	YFH=b0 + b1x0 + b2x1 + b3x0 + b4x0x1 + b5x0x0 = b0 + b2	(5)
女中(FM):	YFM=b0 + b1x0 + b2x0 + b3x0 + b4x0x0 + b5x0x0 = b0	(6)
女低(FL):	YFL=b0 + b1x0 + b2x0 + b3x1 + b4x0x0 + b5x0x1 = b0 + b3	(7)

模型2-7告诉我们如何计算六个组的平均值。为了便于计算它们之间的差别（更重要的是洞察它们之间的结构性关系），我们将模型2-7按以下方式重新安排一下：

表一、性别与教育程度交叉组的回归系数比较

	M（男性）	F（女性）
H（高教育）	b0 + b1 + b2 + b4   (2)	b0 + b2       (5)
M（中教育）	b0 + b1                 (3)	b0              (6)
L（低教育）	b0 + b1 + b3 + b5   (4)	b0 + b3       (7)

根据表一，我们可以很轻松地（目测）算出各组的差别。基于共有六组，共有 6 x 5 / 2 = 15对组组比较，我们用以下的矩阵形式来表示，以省些空间：

表二、组间差别之计算方法

	MH	MM	ML	FH	FM
MM	b2+b4
ML	b2+b4–b3-b5	-b3-b5
FH	b1+b4	b1–b2	b1+b3+b5-b2
FM	b1+b2+b4	b1	b1+b3+b5	b2
FL	b1+b2+b4-b3	b1-b3	b1+b5	b2-b3	-b3
注：所有组间差别均由column group – row group（列标题中的组减去行标题中的组）构成。如MH-MM = b2+b4。如果想求行组减列组，只需将表二中所有系数的符号相反即可。

由表二可知，只有三对组间差别是直接由回归系数告知的 (MM - FM = b1, FH – FM = b2, FM – FL = –b3；注意，这里的b1只反映中等教育程度上男女之间的差别、而不是所有教育程度上的男女差别；b2和b3只反映女性中不同教育程度的差别、而不是所有人中不同教育程度的差别，这就是我前面提到的对主效应系数的一般解释“在有交互影响条件下有问题的”的原因)，而且三者均只涉及主效应系数。另有两对组间差别是由两个主效应系数的组合而成 (MM – FL = b1 – b3, FH – FL = b2 – b3)。其它10对组间差别均涉及主效应和交互项系数的组合。其中尤其是MH - MM的差别，需要同时用到b4和b5两个交互项系数。

这个练习说明什么？既说明交互项系数不等于组间差别、又说明（大部分）组间差别与交互项系数有关系。具体说来，这种“关系”，是附加在主效应系数的基础上产生的，也就是说交互项系数是对一对主效应关系的adjustment（调整）。其调整程度（微调或巨调）则有b4或b5取值决定。

现在，问题解决了吗？也许有些读者还是有点迷糊，觉得名目变量交互分析好麻烦。对的，这就是我一开始说的“技术上容易操作上难”的道理。推而广之，凡涉及名目变量的多元分析（如loglinear modeling、multinomial logistic regression、等等），没有一样不是技术上容易操作上难的。大家要有充分的心理准备。

在本例中，将问题变得相对简单（或容易？）一些的一种方法是不用哑变量编码、而用effects coding（效应编码？）或 contrast coding（配对编码？）。前者用+1定义研究组、-1定义对照组；后者则按一定的限定条件（恕不赘言）来设定任意两组或两集合组（如本例中高教育对中低教育）的比较。由两个效应编码变量构成的交互项反映了在该两个变量上取值为+1的研究组与所有组的（未加权）均值（虽然不一定等于样本均值、但接近“平均”的意思）之差别（如在本例中，可以是男性高教程度与样本“平均”的差别）；由两个配对编码变量构成的交互项则反映了被特定配对的两组或两集合组之间的差别（在这种条件下，交互项系数可以等于组间差别了）。当然，这两种编码（尤其是后者）比哑变量编码在操作上复杂很多、但好处是解读时简单。如果有意学习（或者经常要做）名目变量多元分析的读者，应该花时间分别学一下。（当然，必须说明，不够使用哪种编码方法，交互项的显著性结果是完全一样的。它们的差别只存在于SPSS或其它统计程序输出结果中的系数值，而不同的系数值都是可以互相换算的。）

结束前，为完整起见，需要说明，这里虽然只讨论两个名目变量之间的交互项，其原则可以直接推广到三个或更多个名目变量之间的交互项。

最后，你问如何解读“交互作用項B和EXP(B)”，上面已经讨论了b4-b5的解读。Exp(b)的解读与其相仿，唯一区别在于后者的临界点为1而前者为0，如Exp(b4) > 1或Exp(b5) > 1 反映教育程度的差别在男性中大于女性；相反，如Exp(b4) < 1或Exp(b5) < 1则反映教育程度的差别在男性中小于女性。

如何判断统计显著的差别是否具有实际意义？

丁丁 @ 2009-10-02：

老师，您好！我想问一个关于样本量的基础问题。通常我们有公式可以计算理论最小样本量。但我想问有没有最大样本量，不得因为如果样本量足够大，我可以证明任何没有实际意义的差别是不是statistically significant。比如说，3.75和3.50，SD 都为1.00，如果样本量个为100，不显著。如果是200，就显著了。同理，3.50和3.55，如各有10000，也显著了。但是没有实际意义。我看到很多研究就用这种方法，研究出了很多correlation significant的结果，或两者显著不同的结论。我觉得不对，却没有理论去说它不对。难道真如某人所说, 统计学家可以证明任何事吗?

庄主 @ 2009-10-31:

抱歉，拖了将近一个月才回复你的问题。最近较忙，忙的原因之一是做有关博客写作的可持续性研究（好像就是在研究我自己为什么不能持续写博客）。

你的问题涉及了样本量和统计显著性两个概念，为了理解两者之间的关系，还需要引入其它三个概念：errors in inferential decision（推断决策中的错误）、power of analysis （检验效能）、strength of relationship 或effect size（关系强度或效应规模，注1）。

我们从统计显著性开始，因为大家在看一个统计分析（如相关、回归、方差等）的结果时，总是首先看其显著性（即p值是否小于预设的α值，如 0.05），然后据此而做出相应的推断决策。如p<α则拒绝零假设、p>α则接受零假设。大家知道，尽管有上述p值做依据，这种决策还可能含有误差。如当p<α时，也许零假设还是对的，这时就有犯概率为p的Type I error（型一或“拒真”错误）。相反，如当p>α时，也许零假设却是错的，这时就有犯概率为1 - p的Type II error（型二或“纳伪”错误）。相信大家都看过这些老套的话，但也许不知道这些老土道理是解决很多困惑（包括丁丁的问题）的基本原理。

丁丁关心的是在大样本条件下犯型一错误的可能性。我们先看一下他（她）的例子：有两个均值，分别为3.7和3.5，各自的标准差均为1.0，由于不同样本量而出现了以下两种情况：

一、当N = 100时，两个均值的联合标准误差 = = 0.14（注2），检验两个均值之差的t = (3.7-3.5)/0.14 = 1.41，其相应的p = 0.160（注3）。

二、当N = 200时，两个均值的联合标准误差 = = 0.10，检验两个均值之差的t = (3.7-3.5)/0.10 = 2.00，其相应的p = 0.047。

可见，随着样本的增大，原来不显著的差别现在显著了，这合理吗？就型一错误而言，完全合理。当N = 100时，如果我们拒绝零假设（即3.7 = 3.5），拒真（“真”= 零假设）的风险由16.0%，太大了，不能容忍；而当N = 200时，拒真的风险降为4.7%，在可以容忍的范围内，所以是合理的。

那么，统计上显著的就一定是实际上重要或有意义的吗？自然不是。问题是我们如何判断一个统计显著的结果是重要或有意义？丁丁想知道的大概就是这种判断根据。这种根据，就是我们说的关系之强度或效应之规模（而不是样本最大量问题）。

判断关系强度或效应规模的一个直观（即非正式）准则是两个均值之差要大于均值的十分之一（注4）。如在本例中，均值之差为0.2、远小于均值的十分之一（0.35或0.37，取决于我们以那个均值为比较基准），显然，即使当N = 200时0.2的差别是统计显著的，但其差别还比较小（相对于均值的取值），没有特别的意义。

判断关系强度或效应规模，还有很多更正式的准则，如Pearson’s r（用于关系强度）或Cohen’s d（用于均值之差，注5），两者还可以互相转换（注6）。在本例中，Cohen’s d = 0.2（注7）。按照Cohen的说法，如果d值小于0.3，效应规模为small（小效应）、如果d值在0.5附近，效应规模为medium（中效应），而如果d值在0.8以上效应规模则为large（大效应）。

我们也可以将d转换成Pearson’s r = 0.1。一般说来，r = 0.1 也是一个弱相关。

下图是对以上讨论的一个小结（包括丁丁问题的反面，即如果统计分析的结果不显著时，大样本有什么好处或坏处）。

 

上图也间接回答了丁丁最后引用的问题“统计学家可以证明任何事吗？”。是的，统计学家可以通过提高样本来拒绝零假设，但是，统计学家无法控制关系的强度或效应的规模。如何提高关系的强度或效应的规模？这既是一个理论问题、也是一个（数据收集）方法问题。本庄以前曾有涉及、日后有机会还会讨论，这里就不扯开去了。

注释：

注1：两者同义。关系强度多半用于相关或回归分析而效应规模多半用于方差分析。

注2：丁丁没有交代是两个独立样本还是两个非独立样本，我们假定是前者。

注3：双尾检验。p值可以根据给定的t值和自由度数，用Excel里的TDIST函数求出。

注4：所以一般说来，做社会科学研究的学生最好分别修一门专讲数据收集方法课和一（至数）门统计课。

注5：, 此外还有其它很多与Cohen’s d大同小异的计算均值之差的效应规模的公式。

注6：

注7：算了老半天，d等于均值之差，这是因为两个组的样本量相等，否则会有所不同或很不相同。

为何两个模型的中介变量系数一样？

tan @ 2009-09-14:

祝老师,您好!这个星期的提问我看您都回答了,除了我提的问题。不知是您没注意到还是问题太初级而不值得回答。由于学识粗浅并确实想知道问题的解答，特此再次提问，烦请老师您或其他有识之人给予解惑。

问题是有关用SEM检验中介效应的：变量W和Z为自变量（且W与Z之间没有显著的相关），Y为因变量，X为设想中的中介变量。首先是模型1，只涉及三条路经：W--X；Z--X；X--Y。所有路经系数都显著，模型的拟合度也可接受；接着是模型2，涉及五条路：W--X；Z--X；X--Y；W--Y；Z--Y，即模型2比模型1多了两条路经（W--Y；Z--Y），结果也是所有路经系数都显著，模型的拟合度也可接受。我不可理解的问题是：在模型1和2中，自变量（W和Z）与中介变量（X）的路经系数竟然一样，怎么会这样？但模型1中X--Y的路经系数要大于模型2中X--Y的路经系数。

在此，我想请教的问题是：（1）上述模型（1和2）中，W和Z与X的路经系数有没有可能一模一样？在理论上成立吗？我担心在那个地方做错了。（2）根据您的几个帖子以及其它相关资料，中介效应并不是比较上述我所表述的两个模型的，但在我所学习的Marketing领域，有文献（作者还有一定的名气）却又是这样做的，特别提到：模型2拟合度可接受，所有路经关系都显著，故部分中介效应显著。这样做可以吗？再次感谢！

庄主 @ 2009-09-20:

上周有好几人提了问题，但我没有时间回答所有人的问题，只能按我对问题价值的判断而选择回答部分。我初看你的问题，觉得与8月31日匿名者提的问题相同（见为何不同模型的路径系数和拟合度相同？）。我现在还是这么认为（即，即使不是同一人问的，道理一样）。考虑到读者中也许还有同样的问题，所以再说几句。

为了便于讨论，我将你的两个模型画了出来（建议：很多时候一图胜千字、但这里的提问处不让上传图像，请大家讲图贴在自己的博客或其它公共空间上，然后在你的问题中做个链接）：

问题一、“上述模型（1和2）中，W和Z与X的路经系数有没有可能一模一样？在理论上成立吗？”是否指λ_xw = λ'_xw和λ_xz = λ'_xz？如是，答案是肯定的。一个回归方程的系数当且仅当方程增减自变量时才可能变化。以本案为例，模型a涉及以下两个方程：

X = λ_xwW + λ_xzZ                           (a1)

Y = β_yxX                                      (a2)

而模型b也涉及两个方程：

X = λ'_xwW + λ'_xzZ                         (b1)

Y = β'_yxX + β'_ywW + β'_yzZ              (b2)

如果比较方程a1与b1，可见两者含有同样的自变量（W和Z），所以λ_xw一定等于λ‘_xw，λ_xz也一定等于λ_xz。（注：这是回归分析的基本原理，同样适用于SEM。）

问题二、“模型1中X--Y的路经系数要大于模型2中X--Y的路经系数”。比较方程a2和b2，可见b2比a2多了两个自变量（W和Z），因此β_yx可能不等于β’_yx，条件是(1)W或Z与Y相关（即β'_yw ≠ 0或β'_yz ≠ 0）和 (2) W或和Z与X相关（即λ‘_xw ≠ 0或λ‘_xz ≠ 0）同时成立。既然现在β_yx > β’_yx，说明W或Z两者之中至少一个与X和Y同时相关。（注：这也是回归分析的基本原理。）

问题三、“模型2拟合度可接受，所有路经关系都显著，故部分中介效应显著。这样做可以吗？”模型b的拟合度一定比模型a好，但是由于损失了2个自由度，所以要做统计检验以证明模型b与模型a之间有显著差别。如是，说明模型b更可取。但是，仅比较模型a和模型b而不比较模型b与只含W->Y和Z->的“直接影响模型”（参见如何检验两个中介变量的效应?），确实不是检验中介效应的充要条件 (necessary and sufficient conditions)。为何你们marketing中有“一定名气”的作者这么做？我无法回答，我只知道科学面前人人平等。包括我在内的很多人都相信David Kenny的检验中介变量方法，不是因为他名气大，而是觉得他说的有道理。

如何分析固定样本数据？

H @ 20009-09-08:

我在分析一个固定样本 (panel sample) 的数据，其中每个人被调查了两次，因变量是定距变量、自变量既有定距也有定类变量。我是第一次做Panel，参考了你在《传播统计学》第15章中“固定样本分析的主要步骤”一节，其中建议当因变量为定距变量、自变量即有定距也有定类变量、数据时点为2时，最简便的是使用回归分析、或者使用协方差分析，其结果应该是完全相同的（第405页）。我尝试了SPSS中GLM模型中的Univariate和Repeated Measures两种方法，以下是我用的指令 (其中Y1和Y2是因变量、X是定距自变量、Z是定类自变量)，

UNIANOVA y2 BY z WITH y1 x/Design.

GLM y1 y2 BY z WITH x/WSFACTOR = y 2 Polynomial/WSDESIGN = y/DESIGN.

发现它们的结果并不相同，不知问题出在哪里？

庄主 @ 2009-09-12:

一、你用的UNIANOVA, 正式名字叫做 ANOVA with lagged dependent variable as a covariate（“含有因变量过去值的协方差分析”，简称ANCOVA，也就是我们书上说的协方差分析）。这种方法，与书上公式15-6的OLS regression with lagged department variable as an independent variable（“含有因变量过去值的经典回归分析”），在数学上完全一样，其结果当然也完全一样（参见前文回归与GLM的分析结果真的不同吗？）。

两者相比，协方差分析在操作上有一个好处：可以直接输入定类自变量，而在做回归分析前，则必须先将定类自变量转换成dummy variables (哑变量)。

不管用协方差还是回归分析，最重要的是要明确被检验的零假设是什么？以本例来说，被检验的是以下的零假设：

1. Y1对Y2没有显著影响；

2. X对Y2没有显著影响；

3. Z对Y2没有显著影响。

注意，因为你用的“DESIGN”指令中没有任何自变量，说明你只想检验Y1、X和Z对Y2的main effects（主影响）而不建议三者之间的交互影响，也许这是你的理论问题所需，当然没有问题，而且也简化了这里的讨论。

从这三个假设来看，假设1只是技术性需要（控制Y1与Y2之间的自相关），虽然绝大多数情形下两者会高度相关，但没有什么理论价值，所以不必介意。假设2和3是核心，分别显示在控制了Y1对Y2的影响之后，X和Z各自对Y2有无显著影响（请记住这句话）。

二、你用的GLM，正式名字是Repeated Measures ANCOVA with two dependent variables （“含有因变量前后测量值的协方差分析”，简称RM-ANCOVA）。这种方法与上述的协方差或回归的不同之处在于其将Y1和Y2同时当做因变量，你将其取名为“Y”（注意，这里的Y是只存在于这个协方差分析之中的一个虚拟变量；并注意这个Y与我们书中405页上公式15-5中的因变量ΔY (= Y2 - Y1) 不是一回事，而是与multilevel（多层分析）第一层分析的思路是一致的）。

我们也来看看这里检验的是哪些零假设：

1. Y1与Y2之间没有显著差别 (即一种Test of Within-subjects Effects)；

2. Y1与Y2之间的差别与X没有显著关系（即Y和X对从Y1到Y2变化的交互影响，也是一种Test of Within-subjects Effects）；

3. Y1与Y2之间的差别与Z没有显著关系（即Y和Z对从Y1到Y2变化的交互影响，也是一种Test of Within-subjects Effects）；

4. X对Y（即Y1和Y2的均值）没有显著影响（这是一种Test of Between-subjects Effects）；

5. Z对Y（即Y1和Y2的均值）没有显著影响（也是一种Test of Between-subjects Effects）。

上述零假设中，1与ANCOVA或回归分析的1相仿，检验自相关而已；4和5的意义不大（因为求Y1和Y2的均值没什么理论意义）；假设2和3也是核心，分别检验了X或Z对从Y1到Y2的变化的影响，与ANCOVA的假设2和3分别检验Y2有所不同：前者是一种Within-subjects Effects (前后变化)，而后者是一种Between-subjects Effects（横向比较）。当然，由于两个模型鉴于同样的数据，所以如果X或Z对Y的前后变化没有显著影响时，其对Y2也不会有显著影响。反之亦然。

两者之间，究竟选用那种模型或报告那种结果，取决于你的研究问题。我个人觉得RM-ANCOVA提供的信息更丰富或更接近一般研究问题，但是其结果的解读更复杂，所以需要有对GLM模型比较深入的理解，否则还是以回归分析或ANCOVA为准。

为何不同模型的路径系数和拟合度相同？

Anonymous @ 2009-08-31：

老师您好! 我也刚开始尝试使用SEM做中介效应分析,看了您的几个相关帖子,受益匪浅。恕我愚钝,还有几个问题不明白,还望进一步指教。

1). 您在"如何检验两个中介变量的效应"的帖子中提到：中介效应需要满足三个或者四个条件,其中包括:X或Z(自变量)对Y(因变量)的间接影响大于其直接影响（即 γAX × βYA > βYX 或 γBZ × βYB > βYZ ）。我不明白为什么一定要满足这个条件？如果是这样，是否意味着中介模型中间接效应都大于直接效应，或者说中介效应的比例大于50%。可我经常看到一些文献说，某某变量的中介效应比例为多少多少（低于50%），难道这是错误？

2). 最近我也做了一个中介效应的模型，概念模型类似于6月30日“如何在模型拟合度和模型合理性之间选择？”帖子中的模型。首先用软件跑了模型1，所有系数都显著，模型的拟合度也可接受；接着跑了模型2，结果是所有路径系数也都显著，模型也可接受。我不理解的问题是：a.两个模型不一样，为什么拟合度都可接受；b.两个模型种，W和Z到X的路径系数尽然完全一样，模型都不一样了，怎么路径系数还会相同？其中，X到Y的系数，模型2要比模型1小？C.模型2中，数据显示 βwx * βxy < βwy ,请问这还存在中介效应吗？

不好意思，一下子问了好多问题，也许许多问题还非常初级，见笑了。不慎感激！

庄主 @ 2009-09-05:

1). 为了理解你的问题，我重读了一项原文，发现其中的直接影响符号写错了（现已改正），应该是γ_YX和γ_YZ或而不应该是β_YX和β_YZ（图中的符号是对的）。也就是说，你问题中提到的为何“γAX × βYA > βYX 或 γBZ × βYB > βYZ” 应该是“γAX × βYA > γYX 或 γBZ × βYB > γYZ"。（当然，你对原文的理解没有错。）

我在原文中说过，严格的中介效应模型要求直接影响（即γYX 或 γYZ）彻底消失。这时，间接影响（γAX × βYA或 γBZ × βYB）自然大于直接影响。如果直接影响不等于0但小于间接影响，那么可以认为这是一种让步或妥协的微弱版（weak version）。如果再推一步，直接影响不但不等于0而且大于间接影响，那么直接影响是主流或中心路径(central route)、间接影响只是支流或边缘路径（peripheral route)，那么中介效应的原始意义就大大打折扣了。这是一个理论问题、不是纯粹的统计问题（意思是，间接影响还存在，但没有必要强调其涉及的“mediation process”了）。

我还没看到过你提到的"中介效应的比例大于50%"，是指间接影响的值至少为直接影响的值的一半吗？如果这样，那是对上述微弱版的进一步弱化。

2a). 你的两个模型不同（模型2多了四个系数、少了四个自由度）、但拟合度都可以接受的现象很正常和普遍，因为各自检验的零假设相同，都是模型与数据之间没有显著差别。但是，你还要检验一个零假设，就是两个模型的拟合度之间没有显著差别：如果两者确无差别（即由于增加了间接影响而提高的误拟合度被损失了的自由度所抵消了），则说明间接影响（即中介效应）并不显著；反之则说明存在显著的间接影响（中介效应）。

2b). 你问“两个模型中，W和Z到X的路径系数尽然完全一样，模型都不一样了，怎么路径系数还会相同？”其中的W从何而来？估计你将我另一帖了的符号（其中也许W和Z是自变量、X是中介变量）混着用了。但是如果是这样的话，X不应出现在模型1.而你却说“X到Y的系数，模型2要比模型1小”相矛盾。难以理解。最简单的方法是提供两个表格，一是模型1的变量及其系数、二是模型2的变量及其系数。

2c). 你问的就是：当一个间接影响小于直接影响时，是否还有必要和价值讨论中介效应？我上面已经讨论过。按经典的定义和学术界的主流看法，至少是意义不大。